fMRI解析の基礎 (12):デコーディング
最終更新日: 2020年7月20日
0. はじめに
1. BOLD反応
2. 実験デザイン
3. 前処理
4. GLMの理論
5. GLMと検定
6. 多重比較問題
7. 集団解析
8. 接続性解析
9. コヒーレンス解析
10. 主成分分析
11. 独立成分分析
12. デコーディング
13. エンコーディング
14. 動的因果モデリング
15. 表現類似性分析
デコーディングとは?
観察したBOLD反応から刺激を予測すること。
最も広く使われているデコーディング手法は、Multivoxel Pattern Analysis (MVPA) というパターン分類手法です。
1. 概観
例として、Haxvy et al. (2001) のような2つのカテゴリー1の写真を呈示する Slow Event-Related Design の実験について考えます。刺激に反応する腹側側頭皮質のBOLD反応を分類しましょう。
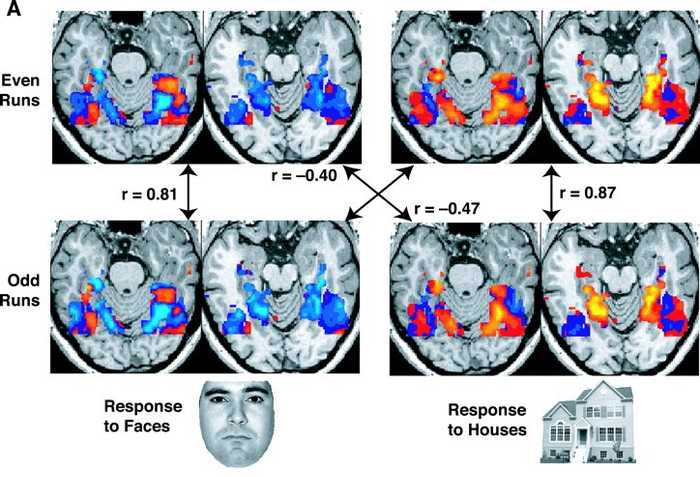
(Haxvy et al. (2001) より引用)
この反応を写真呈示後のいくつかの TR にかけて和をとり、activity vector とします。 activity vector を特徴量として、以下の手順で分類器の学習と評価をします。
- training set と validation set に分ける。
- 分類器を選ぶ。
- training set で分類器を訓練する。
- 分類器の予測性能を、validation set で評価する。
Haxvy et al. (2001) では、2つのカテゴリーを良い精度で分類することができました。MVPAは、2つのカテゴリー間の脳活動のような微妙な効果もカバーすることができます。
2. 探索領域と次元の呪い
探索領域は、小さすぎると多変量の良さが無くなってしまいますが、大きすぎても以下の問題があります。
- 統計的に有効であっても、理論的な貢献は小さくなってまう。
- MVPAアルゴリズムの計算速度が低下する。
- 次元の呪いを受ける。高次元では距離の尺度が複雑になり、距離で判別する分析手法は難易度が上昇する。
3. 活性化ベクトル
BOLD反応は約25秒続くので、時間の扱い方は重要となります。全てのボクセルに1つの要約値を与える方法と、経時変化を表現するベクトルを与える方法が考えられます。
Block Design では、最初のTRを除いて平均BOLD反応を計算することが多いです。
Slow Event-Related Design では、使われる代表値はいいろいろあります。ピークの和、20 -25 秒間の和、GLMの回帰係数などが使われます。
Rapid Event-Related Design では、BOLD反応の重なりや共線性から代表値の計算は困難になります。Mumford et al. (2012) では、各イベントごとに one-hot vector を作って回帰係数 を割り当てる方法を提案しました(下図のLS1)。
一方、Turner et al. (2012) では、one-hot vector の代わりに FBR法を用いて同様のパフォーマンスを示しました(下図のFS)。この方法は、重ね合わせを考慮できている利点があります。
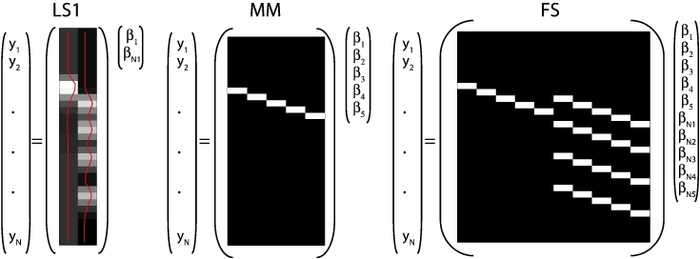
(Turner et al. (2012) より引用)
4. MVPAのための前処理
スムージングが有効かどうかは、ケースバイケースです。Hyperacuity と呼ばれる「サブクラスタへの鋭敏さ」に依存するようです。
標準化によって微妙な変化に対する敏感さは上昇します。しかし、クラス間に大きな平均の差がある場合は、それを小さくしてしまうという欠点があります。
これを克服するために、control standardization と呼ばれる、クラス情報を使って標準化する方法が提案されています (Linn et al. (2016))。
5. 分類器の作成
分類器には2つのタイプがあり、一般的には、**Deterministic classifiers(決定論的分類器)**が使われます。
- Deterministic classifiers:0 か 1 を出力する。
- Probabilistic classifiers:確率を出力する。
分類器の分類方法に関しても、大きく2つに分類できます。
- Linear classifiers :線形分離可能なデータに対して有効。
- Nonlinear classifiers:非線形な決定境界にも適用可能。表現力が高い代わりに過学習しやすい・解釈しづらいといった欠点もある。

多クラス分類には以下の2つがあります。
- 1-of-K classifiers:2クラス分類器を個使う。(1 vs その他)
- 1-of-1 classifiers:2クラス分類器を 個使う。(1 vs 1 を全通り)
例1. Fisher Linear Discriminant Analysis
各クラス内の特徴量が多変量正規分布に従うときに最適な手法です。
上の境界関数に対し、以下が成立します。
理解しやすく高度な数値最適化が必要ないのですが、次元の呪いを受けやすいです。
例2. Support Vector Machines
MVPAの最も人気な分類器で、効率よく高次元空間の決定境界を探索できます。具体的には、サポートベクトルの存在する2つの平面の間のマージンを最大化するような平面を探索します2。
SVMは、線形・非線形のどちらにもなります。最も有名なガウシアンカーネルを使った方法では、データをD次元の空間から無限次元の空間に投射し、どんなデータでも線形分離可能とすることができます。
6. 分類器の評価
再現性の確保のために、正確な精度の推定が重要となります。分類器の最適なパラメータを決め、それを用いて検証をします。
問題となるのは、検証データの分割方法です。fMRI データはサンプル数が少ないことが多く、学習に多くのサンプルを使うとバリアンスが大きくなり、検証に多くのサンプルを使うとバイアスが大きくなります(バイアスーバリアンスのトレードオフ3)。
そこで、これを和らげるために、交差検証 (CV) をします。交差検証では、バイアスを小さくするために、クラスの割合を均等に階層化する必要があります。Leave-one-out CV は、バイアスを最も小さくできますが、計算時間の問題も生じます。Leave-1run-out CV は、実験の構造を保持することができるという利点があります。
7. 統計的推論
1st Level
各々のクラスに対しての交差検証精度は、
となります。
あるボリュームが異なるイベントに対して異なる反応をしているかどうかは、以下で検定できます。ただし、= chance rate、= false positive rate です。
複数のボリュームに対してこれを行うときは多重比較問題が出てきます。
2nd Level
被験者間で活性化パターンが違うことが多々あります。Hyperalignmentでは、活性化パターンを重ね合わせることでこれを調整します (Haxby et al. (2011))。
- 各被験者の複数のイベントに対する activvitty vector を並べる。
- 揃えるためのテンプレートをランダムに1つ選びとして、以下のとの差を最小化するように変換行列を決定する。
仮説検定の他に、順列検定を使うのも適しています。ラベルを張り替えるだけで時系列などの統計的情報を変化させずに検定が行えます。
8. 特徴量選択
最も有益な特徴量を選択することを特徴量選択といいます。教師あり特徴量選択をする場合は、精度の検証データとは異なるデータでやる必要があるため、分割は3つになります。
教師あり特徴量選択
- Filter: 学習はしない。ラベルとの相関やt検定などで、有効な領域を選択する。
- Wrapper: 学習に効く領域を選択する。学習した重みの大きさを元に選択を繰り返す方法は Recursive Feature Elimination (RFE) と呼ばれる。
教師なし特徴量選択
- PCA
- ICA
Reference
- Ashby, F. G. (2019). Statistical analysis of fMRI data. MIT press. url
- Haxby, J. V., Gobbini, M. I., Furey, M. L., Ishai, A., Schouten, J. L., & Pietrini, P. (2001). Distributed and overlapping representations of faces and objects in ventral temporal cortex. Science, 293(5539), 2425-2430. url
- Mumford, J. A., Turner, B. O., Ashby, F. G., & Poldrack, R. A. (2012). Deconvolving BOLD activation in event-related designs for multivoxel pattern classification analyses. Neuroimage, 59(3), 2636-2643. url
- Turner, B. O., Mumford, J. A., Poldrack, R. A., & Ashby, F. G. (2012). Spatiotemporal activity estimation for multivoxel pattern analysis with rapid event-related designs. NeuroImage, 62(3), 1429-1438. url
- Linn, K. A., Gaonkar, B., Satterthwaite, T. D., Doshi, J., Davatzikos, C., & Shinohara, R. T. (2016). Control-group feature normalization for multivariate pattern analysis of structural MRI data using the support vector machine. NeuroImage, 132, 157-166. url
- Haxby, J. V., Guntupalli, J. S., Connolly, A. C., Halchenko, Y. O., Conroy, B. R., Gobbini, M. I., ... & Ramadge, P. J. (2011). A common, high-dimensional model of the representational space in human ventral temporal cortex. Neuron, 72(2), 404-416. url
- 顔と物体の2つのカテゴリー。↩
- サポートベクトルマシンとサポートテンソルマシン:SVM・STMでも解説しています。↩
- 簡単に言うと、バイアスは「モデルの適合度」、バリアンスは「モデルの複雑さ」。脳画像解析における交差検証と精度誤差についてやPRML3章(2)バイアスバリアンス分解とベイズ線形回帰でも解説しています。↩