PRML３章（２）バイアスバリアンス分解とベイズ線形回帰

最終更新日: 2020年5月29日

Jupyter Notebookはこちら

バイアスーバリアンス分解：モデルの複雑さの問題

モデルの複雑さの問題として... バイアス-バリアンスのトレードオフ

損失関数：二乗損失関数 $L={(t-y( \vec{x}))}^2$

最適な予測：条件付き期待値 $h(\vec{x})=\mathbb{E}[t|\vec{x}]=\int t p(t|\vec{x})dt$

二乗損失の期待値（＝平均的な誤差）を計算しましょう。

\mathbb{E}[L] = \int \{y(\vec{x})-h(\vec{x})\}^2 p(\vec{x})d\vec{x} + \int \int \{h(\vec{x})-t\}^2 p(\vec{x},t) d\vec{x} dt

一項目から、

\{y(\vec{x};D)-h(\vec{x})\}^2 = \{y(\vec{x};D)-\mathbb{E}_D[y(\vec{x};D)]+\mathbb{E}_D[y(\vec{x};D)]-h(\vec{x})\}^2 \\ = (y-\mathbb{E}_D)^2+(\mathbb{E}_D-h)^2+2(y-\mathbb{E}_D)(\mathbb{E}_D-h)

\therefore \ \mathbb{E}_D[\{y(\vec{x};D)-h(\vec{x})\}^2] = (\mathbb{E}_D-h)^2 + \mathbb{E}_D[(y-\mathbb{E}_D)^2]

と表されます。これは以下の関係を表しています。

二乗損失の期待値＝(バイアス)^2+(バリアンス)+(ノイズ)

バイアス：「データによる平均的な予測」と「最適な予測」とのずれであり、モデルが複雑なほど減少します。
バリアンス：「データによる予測」と「データによる平均的な予測」とのずれであり、モデルが複雑なほど増大します。

したがって、モデルの複雑さを制御し、**バイアスとバリアンスをバランスよく小さくする**ことで、過学習を防ぐことができます。

ベイズ線形回帰

ベイズ的に扱うことで、モデルの複雑さを回避します。

Liklihood : $p(\vec{t}|\vec{w}) = \prod_{ n = 1 }^N \mathcal{N}(t_n|\vec{w}^T\vec{\phi}(\vec{x_n}),\beta^{-1})$

Prior : $p(\vec{w})=\mathcal{N}(\vec{w}|m_0,S_0)$

Posterior : $p(\vec{w}|\vec{t}) \propto p(\vec{t}|\vec{w})p(\vec{w})$

したがって、今までの結論から、

p(\vec{w}|\vec{t}) = \mathcal{N}(\vec{w}|\vec{m_N},S_N)

となります。ただし、

\left\{ \begin{array}{l} \vec{m_N}=S_N(S_0^{-1}m_0+\beta\Phi^T\vec{t}) \\ S_N = S_0^{-1}+\beta\Phi^T\Phi \end{array} \right.

となります。簡単にするため、等方的ガウス分布を用いて、

p(\vec{w})=p(\vec{w}|\alpha)=\mathcal{N}(\vec{w}|0,\alpha^{-1}I)

とすると、

\left\{ \begin{array}{l} \vec{m_N}=\beta S_N\Phi^T\vec{t} \\ S_N = \alpha I+\beta\Phi^T\Phi \end{array} \right.

となるので、事後分布の対数は、

\ln p(\vec{w}|\vec{t}) = - \left[ \frac{\beta}{2} \sum_{n=1}^N \{ t_n -\vec{w}^T\vec{\phi} \} +\frac{\alpha}{2}\vec{w}^T\vec{w} \right] + (定数)

となります。したがって、事後分布を最大化するためには、[　]内を最小化すればよいでしょう。

予測分布：新しい $\vec{x}$ に対する $t$ の確率分布（不確かさ）を予測する。

p(t_{new}|\vec{t};\alpha,\beta)= \int p(t_{new}|\vec{w};\beta)p(\vec{w}|\vec{t};\alpha,\beta) d \vec{w}

= \mathcal{N}(t_{new}|\vec{m_N}^T \vec{\phi}(x_{new}),\sigma_N^2(x_{new}) )

ただし、 $\sigma_N^2(x_{new})=\frac{1}{\beta}+\vec{\phi}^T S_N \vec{\phi}$ となり、これは（ノイズ）+（ $\vec{w}$ の不確かさ）を表しています。

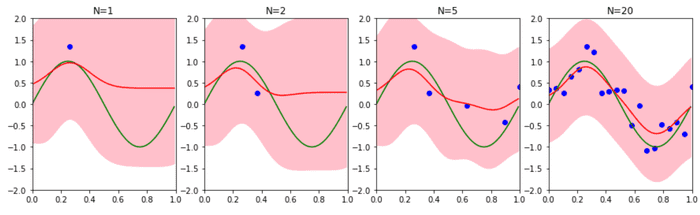
▷ データ点の近傍で不確かさは最小となります。データ数を増やせば不確かさが減ります。

$\alpha, \beta = 1.0$ としたときのベイズ回帰の Python による実装は以下です。データ点と不確かさの関係が確認できます。

alpha=1.0
beta=1.0
N = 20
M = 10
ary_mu = np.linspace(0,1,M)

x_real = np.arange(0, 1, 0.01)
y_real = np.sin(2*np.pi*x_real)

x_train = np.linspace(0,1,N)
y_train =  np.sin(2*np.pi*x_train) + np.random.normal(0,0.3,N)

def phi(mus, x):
    ret = np.array([np.exp(-(x-mu)**2/(2*0.1**2)) for mu in mus])
    ret[0] = 1
    return ret

def pred(x_train, y_train,ax):
    N = x_train.shape[0]
    PHI = np.array([phi(ary_mu,x) for x in x_train]).reshape(N,M)

    S = inv(alpha * np.identity(M) + beta * (PHI.T).dot(PHI))
    m = beta * (S.dot(PHI.T).dot(y_train.T))

    PHI_real = np.array([phi(ary_mu,x) for x in x_real]).reshape(100,M)
    pred_mean = PHI_real.dot(m)
    pred_std = np.sqrt(1.0/beta + np.diag(PHI_real.dot(S).dot(PHI_real.T)))

    ax.plot(x_train, y_train, 'bo')
    ax.plot(x_real, y_real, 'g-')
    ax.plot(x_real, pred_mean, 'r-')
    ax.fill_between(x_real, pred_mean+pred_std, pred_mean-pred_std, color='pink')
    ax.set_xlim(0.0, 1.0)
    ax.set_ylim(-2, 2)
    ax.set_title("N={}".format(N))

f,axes = plt.subplots(1,4,figsize=(15,4))
r = np.arange(N)
np.random.shuffle(r)
for i,k in enumerate((1, 2, 5, N)):
    indices = np.sort(r[0:k]) 
    pred(x_train[indices], y_train[indices],axes[i])

等価カーネル（平滑化行列）

今までの結果を回帰式に代入すると、

y(\vec{x},\vec{m_N}) = \vec{m_N}^T\vec{\phi} = \beta \vec{\phi}S_N\Phi^T\vec{t}=\sum_{n=1}^N \beta \vec{\phi}S_N\phi(\vec{x_n})t_n

\therefore y(\vec{x},\vec{m_N})=\sum_{n=1}^Nk(\vec{x},\vec{x_n})t_n

と表せます。この $k(\vec{x},\vec{x_n})$ を**等価カーネル**といい、2つ以上の $x$ に対する $y$ の事後分布同士の不確かさを決めます。

Reference

Bishop, Christopher M. Pattern recognition and machine learning. springer, 2006.