fMRI解析の基礎 (15)：表現類似性分析

最終更新日: 2020年7月21日

fMRI解析の基礎シリーズ

表現類似性分析 (Representational Similarity Analysis, RSA) とは、多変量解析によって脳活動の類似性構造を抽出する方法です。下図の例では、物体のカテゴリーごとに類似した脳反応のあることがわかります。

RSAの例
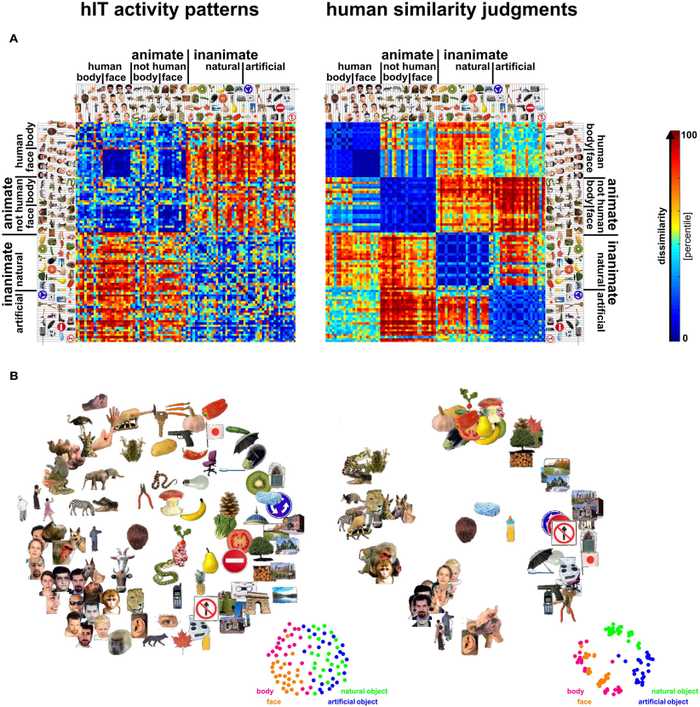
（Mur et al. (2013) より引用）

BOLD反応の類似性構造は、知識的な類似性構造と共通点の多いことがわかっています。これは、類似性構造の比較でのみ評価ができます。

まず、RDM (Representational Dissimilarity Matrix) という、全組み合わせの非類似性を示す行列を以下の手順で作成します。

ROI を決める。
- 次元の呪いは、あまり深刻ではない。イベントタイプ数より少ない次元を選択すると良い。
活性化パターンを定量化する。
- １つのイベントにつき１つの活性化パターンを同定すればよい。各ボクセルに対しGLMを行えば、回帰係数によって定量化できる。
パターン間の非類似性を定量化する。
- 各イベントの組み合わせについて非類似性 $d(E_i,E_j)$ を求める。この尺度は、距離のように２点の順序に不変でなくても良い。

非類似性として主に使われる尺度には、次のようなものがあります。

ピアソン相関
- $d(E_i,E_j) = 1 - r(\beta_i,\beta_j)$ (Kriegeskorte et al. (2008))
- $d(E_i,E_j) = -\ln[r(\beta_i,\beta_j)]$ (Shepard (1987))
ユークリッド距離
- $d(E_i,E_j) = (\beta_i-\beta_j)^T(\beta_i-\beta_j)$
マハラノビス距離
- $d(E_i,E_j) = (\beta_i-\beta_j)^T\hat{\Sigma}_s^{-1}(\beta_i-\beta_j)$
- 多変量正規分布に従う分散共分散行列 ${\Sigma}_s$ を推定しなくてはならない。

これはGLMで行える。（Monahan (2008)）

\hat{\Sigma}_s^{-1}=\frac{1}{N_{TR}-rank(X)}(Y-X \hat{B})^T(Y-X \hat{B})

S-fold 交差検証距離
- $d(E_i,E_j) = \frac{1}{S}\sum_{k=1}^S(\beta_{i,k}-\beta_{j,k})^T\hat{\Sigma}_s^{-1}(\beta_{i,-k}-\beta_{j,-k})$

多次元尺度構成法 (MDS) を用いて、RDMから低次元空間上に移したときの座標を計算できます（最初の図のB）。以下の手順で行います。

ランダムな初期値の設定
全ての２点間距離の計算
非類似性と距離の比較
- Metric：線形となっているので、線形回帰する。
- NonMetric：順序を保持する関数 $f$ を通して、非類似性と距離の順序を固定し、スケーリングした二乗和誤差を最小化する。

埋め込み空間の最適な次元はわかりません。エルボー法で見つけます。

一般的には、求めた類似性構造を人の好感尺度などによるRDMと比較します。これは、心理学的な理論において、心理的空間上の構造は知覚構造と解釈できるということからも妥当性があります。

人間の判断は、次の距離の公理を大きく違反することがあります。そのため、バイアスに注意する必要があります。

Equal self-similarity ( 同一性 ) : $d(E_i,E_i)=d(E_j,E_j)=0$
Minimarity ( 非負性 ) : $\forall E_i \ne E_j \Rightarrow d(E_i,E_j) \gt d(E_i,E_i)$
Symmetry ( 対称性 ) : $d(E_i,E_j)=d(E_j,E_i)$
Triangle inequality ( 三角不等式 ) : $d(E_i,E_j)+d(E_j,E_k) \ge d(E_i,E_k)$

一般的な方法としては、被験者ごとのRDMを平均した行列に対しMDSを行う方法があります。

他にも、INDSCALモデルを用いて、「被験者ごとにいろいろなMDS次元への注意にばらつきがある」と仮定して推定することもできます。

２つのRDMの類似性の順位相関統計的な基準は主に２つあります。RSMでは、ケンドールの $\tau$ の方が適しているとされています。

２つのRDMが統計的に有意に異なるかを検定するためには、順列検定を用いるのが良いとされます。繰り返しラベルを張り替えて順位相関係数を計算することで、目的の仮説のp値を算出します。

モデルベース（Encoding）の予測BOLDによるRDMと、BOLDによるRDMを比較します。これによって、エンコーディングモデルを検証できます。

\hat{B}(E_i)= \frac{\sum_{k \ne i} r(E_i,E_k)B(E_k)}{\sum_{k \ne i} r(E_i,E_k)} \\ B(E_i): \text{BOLD of event } i, \ \ r(\cdot, \cdot): \text{Corrleation}

類似性に基づいて分類することで、デコーディングにも利用できます。

Ashby, F. G. (2019). Statistical analysis of fMRI data. MIT press. url
Mur, M., Meys, M., Bodurka, J., Goebel, R., Bandettini, P. A., & Kriegeskorte, N. (2013). Human object-similarity judgments reflect and transcend the primate-IT object representation. Frontiers in psychology, 4, 128. url
Kriegeskorte, N., Mur, M., & Bandettini, P. A. (2008). Representational similarity analysis-connecting the branches of systems neuroscience. Frontiers in systems neuroscience, 2, 4. url
Shepard, R. N. (1987). Toward a universal law of generalization for psychological science. Science, 237(4820), 1317-1323. url
Monahan, J. F. (2008). A primer on linear models. CRC Press.
Anderson, A. J., Zinszer, B. D., & Raizada, R. D. (2016). Representational similarity encoding for fMRI: Pattern-based synthesis to predict brain activity using stimulus-model-similarities. NeuroImage, 128, 44-53. url