コヒーレンス解析では、周波数領域における相関関係 を利用して接続性を解析します 。
この利点は、HRFの違いに影響されないこと 、ノイズに影響されないこと です。つまり、これまでの接続性解析法 。
1. 自己相関と相互相関
コヒーレンス解析における基本統計量は、自己相関関数 A ( t ) A(t) A ( t ) 相互相関関数 C ( t ) C(t) C ( t )
A 1 ( t ) = E [ y 1 ( T + t ) y 1 ( T ) ] C 12 ( t ) = E [ y 1 ( T + t ) y 2 ( T ) ] \begin{array}{rcl}
A_1(t) &=& \mathbb{E}[y_1(T+t)y_1(T)] \\
C_{12}(t) &=& \mathbb{E}[y_1(T+t)y_2(T)]
\end{array} A 1 ( t ) C 12 ( t ) = = E [ y 1 ( T + t ) y 1 ( T )] E [ y 1 ( T + t ) y 2 ( T )] 自己相関関数と相互相関関数は、以下のような指標となっています。
自己相関関数:時刻 T T T T + t T+t T + t 。
相互相関関数:ラグを T T T 。
わかりやすい解説
2. パワースペクトルとクロススペクトル
スペクトル解析では、各周波数帯の信号密度を計算することで、時系列信号を周波数領域に変換します。このとき、フーリエ変換を用いて周波数領域への変換を行います 。
自己相関関数 A ( t ) A(t) A ( t ) パワースペクトル P ( f ) P(f) P ( f )
P 1 ( f ) = F [ A 1 ( t ) ] = ∫ − ∞ ∞ exp [ − i 2 π f t ] A 1 ( t ) d t P_1(f) = \mathcal{F}[A_1(t)] = \int_{-\infty}^{\infty} \exp[-i2 \pi ft] A_1(t) dt P 1 ( f ) = F [ A 1 ( t )] = ∫ − ∞ ∞ exp [ − i 2 π f t ] A 1 ( t ) d t オイラーの公式 exp [ i θ ] = cos θ + i sin θ \exp[i \theta] = \cos \theta + i \sin \theta exp [ i θ ] = cos θ + i sin θ
P 1 ( f ) = ∫ − ∞ ∞ cos ( 2 π f t ) A 1 ( t ) d t + i ∫ − ∞ ∞ sin ( 2 π f t ) A 1 ( t ) d t P_1(f) = \int_{-\infty}^{\infty} \cos (2\pi ft) A_1(t) dt + i \int_{-\infty}^{\infty} \sin (2\pi ft) A_1(t) dt P 1 ( f ) = ∫ − ∞ ∞ cos ( 2 π f t ) A 1 ( t ) d t + i ∫ − ∞ ∞ sin ( 2 π f t ) A 1 ( t ) d t と分解できます。これを a + b i a+bi a + bi f f f 振幅 は a 2 + b 2 \sqrt{a^2+b^2} a 2 + b 2 位相 は tan − 1 ( b / a ) \tan^{-1}(b/a) tan − 1 ( b / a ) A ( t ) A(t) A ( t ) A ( − t ) = A ( t ) A(-t) = A(t) A ( − t ) = A ( t ) sin ( θ ) \sin(\theta) sin ( θ ) 0 0 0 パワースペクトルは必ず実数値となります 。
一方、相互相関関数 C ( t ) C(t) C ( t ) クロススペクトル密度関数 S ( f ) S(f) S ( f )
S 12 ( f ) = F [ C 12 ( t ) ] = ∫ − ∞ ∞ exp [ − i 2 π f t ] C 12 ( t ) d t S_{12}(f) = \mathcal{F}[C_{12}(t)] = \int_{-\infty}^{\infty} \exp[-i2 \pi ft] C_{12}(t) dt S 12 ( f ) = F [ C 12 ( t )] = ∫ − ∞ ∞ exp [ − i 2 π f t ] C 12 ( t ) d t パワースペクトルとは違って、クロススペクトル密度関数は複素数となります 。そのため、絶対値を取ることでクロスパワースペクトル P ( f ) P(f) P ( f )
P 12 ( f ) = ∣ S 12 ( f ) ∣ P_{12}(f) = |S_{12}(f)| P 12 ( f ) = ∣ S 12 ( f ) ∣ わかりやすいスライド
3. コヒーレンス
コヒーレンス解析では、位相の情報を無視して振幅のみの相関係数の二乗 を測定することになります。ある周波数におけるコヒーレンス coh ( f ) \text{coh}(f) coh ( f ) 。
coh 12 ( f ) = [ P 12 ( f ) ] 2 P 1 ( f ) P 2 ( f ) \text{coh}_{12}(f) = \frac{[P_{12}(f)]^2}{P_{1}(f)P_{2}(f)} coh 12 ( f ) = P 1 ( f ) P 2 ( f ) [ P 12 ( f ) ] 2 コヒーレンス coh ( f ) \text{coh}(f) coh ( f ) 0 ≤ coh ( f ) ≤ 1 0 \le \text{coh}(f) \le 1 0 ≤ coh ( f ) ≤ 1 周波数領域における y 1 ( t ) y_1(t) y 1 ( t ) y 2 ( t ) y_2(t) y 2 ( t ) 。コヒーレンスが大きい場合、1 / f 1/f 1/ f
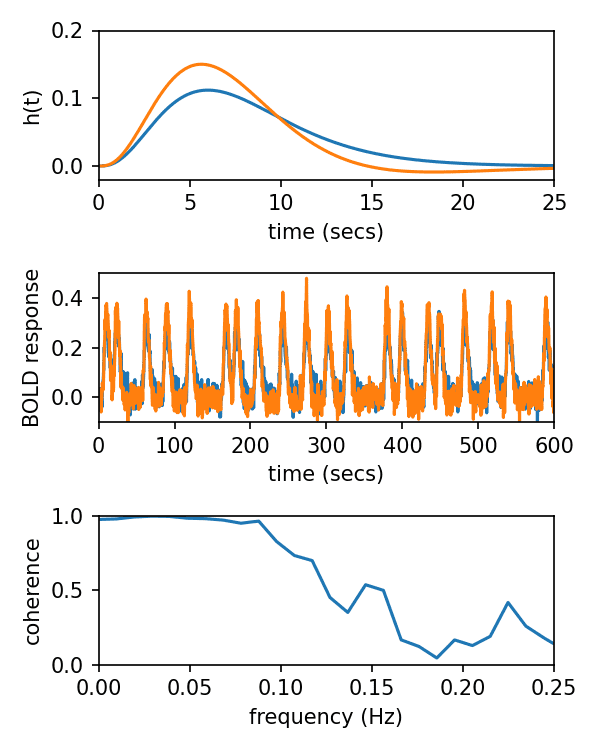
高周波数帯ではノイズの影響によってコヒーレンスは低下します。また、HRFの遅さによって高周波成分は大きく減衰します。つまり、HRFはローパスフィルタとしてはたらきます。そのため、低周波数帯におけるコヒーレンスが重要 となります。
ただし、0 Hz付近ではどんな信号同士もコヒーレンスが高くなってしまう ため、経験的には 0.1 - 0.2 Hz のコヒーレンスを使うとよいとされます。
ここで、HRFの違いによるコヒーレンスの違い を考えてみます .。神経活動 N 1 ( t ) , N 2 ( t ) N_1(t), N_2(t) N 1 ( t ) , N 2 ( t ) h 1 ( t ) , h 2 ( t ) h_1(t), h_2(t) h 1 ( t ) , h 2 ( t ) y 1 ( t ) , y 2 ( t ) y_1(t), y_2(t) y 1 ( t ) , y 2 ( t )
y 1 ( t ) = N 1 ( t ) ⊗ h 1 ( t ) y 2 ( t ) = N 2 ( t ) ⊗ h 2 ( t ) y_1(t) = N_1(t) \otimes h_1(t) \\
y_2(t) = N_2(t) \otimes h_2(t) y 1 ( t ) = N 1 ( t ) ⊗ h 1 ( t ) y 2 ( t ) = N 2 ( t ) ⊗ h 2 ( t ) これをフーリエ変換します。ここで、H ( t ) H(t) H ( t )
F [ y 1 ( t ) ] = F [ N 1 ( t ) ] ∗ H 1 ( f ) F [ y 2 ( t ) ] = F [ N 2 ( t ) ] ∗ H 2 ( f ) F [ y 1 ( t ) y 2 ( t ) ] = F [ N 1 ( t ) ] ∗ H 1 ( f ) ∗ F [ N 2 ( t ) ] ∗ H 2 ( f ) \begin{array}{l}
\mathcal{F} [y_1(t)] = \mathcal{F} [N_1(t)] * H_1(f) \\
\mathcal{F} [y_2(t)] = \mathcal{F} [N_2(t)] * H_2(f) \\
\mathcal{F} [y_1(t) y_2(t)] = \mathcal{F} [N_1(t)] * H_1(f) * \mathcal{F} [N_2(t)] * H_2(f)
\end{array} F [ y 1 ( t )] = F [ N 1 ( t )] ∗ H 1 ( f ) F [ y 2 ( t )] = F [ N 2 ( t )] ∗ H 2 ( f ) F [ y 1 ( t ) y 2 ( t )] = F [ N 1 ( t )] ∗ H 1 ( f ) ∗ F [ N 2 ( t )] ∗ H 2 ( f ) したがって、コヒーレンスは以下のように示されます。
coh 12 ( f ) = [ P 12 ( f ) ] 2 P 1 ( f ) P 2 ( f ) = [ P N 1 N 2 ( f ) ∣ H 1 ( f ) ∣ ∣ H 2 ( f ) ∣ ] 2 P N 1 ( f ) ∣ H 1 ( f ) ∣ P N 2 ( f ) ∣ H 2 ( f ) ∣ = [ P N 1 N 2 ( f ) ] 2 [ P N 1 ] [ P N 2 ] ( ← H がなくなった ) \begin{array}{rcl}
\text{coh}_{12}(f) &=& \frac{[P_{12}(f)]^2}{P_{1}(f)P_{2}(f)} \\
&=& \frac{[P_{N_1N_2}(f)|H_1(f)||H_2(f)|]^2}{P_{N_1}(f)|H_1(f)|P_{N_2}(f)|H_2(f)|} \\
&=& \frac{[P_{N_1N_2}(f)]^2}{[P_{N_1}][P_{N_2}]}
\ \ (\leftarrow Hがなくなった)
\end{array} coh 12 ( f ) = = = P 1 ( f ) P 2 ( f ) [ P 12 ( f ) ] 2 P N 1 ( f ) ∣ H 1 ( f ) ∣ P N 2 ( f ) ∣ H 2 ( f ) ∣ [ P N 1 N 2 ( f ) ∣ H 1 ( f ) ∣∣ H 2 ( f ) ∣ ] 2 [ P N 1 ] [ P N 2 ] [ P N 1 N 2 ( f ) ] 2 ( ← H がなくなった ) ということで、コヒーレンスはHRFに依存せず、神経活動の相関を測定できる といえます 。
最後に、コヒーレンスの検定 をします。帰無仮説 H 0 \text{H}_0 H 0 H 1 \text{H}_1 H 1 H 0 \text{H}_0 H 0 D D D
H 0 : coh 12 ( f ) = coh 34 ( f ) H 1 : coh 12 ( f ) > coh 34 ( f ) D = tanh − 1 [ coh 12 ( f ) ] − tanh − 1 [ coh 34 ( f ) ] If H 0 is true, D ∼ N ( 0 , σ c 2 ) \begin{array}{l}
\text{H}_0: \text{coh}_{12}(f) = \text{coh}_{34}(f)\\
\text{H}_1: \text{coh}_{12}(f) \gt \text{coh}_{34}(f)\\
D = \tanh^{-1} [\text{coh}_{12}(f)] - \tanh^{-1} [\text{coh}_{34}(f)] \\
\text{If H}_0 \text{is true, } D \sim \mathcal{N} (0, \sigma_c^2)
\end{array} H 0 : coh 12 ( f ) = coh 34 ( f ) H 1 : coh 12 ( f ) > coh 34 ( f ) D = tanh − 1 [ coh 12 ( f )] − tanh − 1 [ coh 34 ( f )] If H 0 is true, D ∼ N ( 0 , σ c 2 ) 4. 偏コヒーレンス
刺激によって2つの領域が同時に活性化する場合、これらの領域間の接続性はどのように測定すれば良いのでしょうか?ここでは、偏相関係数 ρ 12 ⋅ 3 \rho_{12 \cdot 3} ρ 12 ⋅ 3 。
ρ 12 ⋅ 3 = ρ 12 − ρ 13 ρ 23 1 − ρ 13 2 1 − ρ 23 2 \rho_{12 \cdot 3} = \frac{\rho_{12} - \rho_{13}\rho_{23}}{\sqrt{1-\rho_{13}^2}\sqrt{1-\rho_{23}^2}} ρ 12 ⋅ 3 = 1 − ρ 13 2 1 − ρ 23 2 ρ 12 − ρ 13 ρ 23 これをコヒーレンス解析に適用すると、偏コヒーレンス coh 12 ⋅ 3 ( f ) \text{coh}_{12 \cdot 3} (f) coh 12 ⋅ 3 ( f ) 。
coh 12 ⋅ 3 ( f ) = [ coh 12 ( f ) − coh 13 ( f ) coh 23 ( f ) 1 − coh 13 ( f ) 1 − coh 23 ( f ) ] 2 \text{coh}_{12 \cdot 3} (f) = \left[ \frac{\sqrt{\text{coh}_{12}(f)} - \sqrt{\text{coh}_{13}(f)}\sqrt{\text{coh}_{23}(f)}}{\sqrt{1-\text{coh}_{13}(f)}\sqrt{1-\text{coh}_{23}(f)}} \right]^2 coh 12 ⋅ 3 ( f ) = [ 1 − coh 13 ( f ) 1 − coh 23 ( f ) coh 12 ( f ) − coh 13 ( f ) coh 23 ( f ) ] 2 Sun et al. (2004) では、領域3の信号として、刺激から生成する理想的なBOLD信号を利用することを勧めています 。
5. 位相スペクトルと因果
一般的なコヒーレンス解析では、領域間の相関関係を測定しているだけであり、因果関係はわかりません。しかし、位相に注目すると因果関係が1 → \to → 。
神経活動の時間遅れを τ \tau τ φ \varphi φ 。
N 1 ( t ) = N 2 ( t − τ ) φ 12 = arg [ S 12 ( f ) ] = ∫ − ∞ ∞ cos ( 2 π f t ) C 12 ( t ) d t ∫ − ∞ ∞ sin ( 2 π f t ) C 12 ( t ) d t ∴ τ = − ( 1 / 2 π ) d d f φ 12 ( f ) \begin{array}{l}
N_1(t) = N_2(t - \tau) \\
\varphi_{12} = \arg [S_{12}(f)] = \frac{\int_{-\infty}^{\infty} \cos (2\pi ft) C_{12}(t) dt}{\int_{-\infty}^{\infty} \sin (2\pi ft) C_{12}(t) dt} \\
\therefore \tau = - (1/2\pi) \frac{d}{df} \varphi_{12}(f)
\end{array} N 1 ( t ) = N 2 ( t − τ ) φ 12 = arg [ S 12 ( f )] = ∫ − ∞ ∞ s i n ( 2 π f t ) C 12 ( t ) d t ∫ − ∞ ∞ c o s ( 2 π f t ) C 12 ( t ) d t ∴ τ = − ( 1/2 π ) df d φ 12 ( f ) 実際には、位相スペクトルを計算して数値的に勾配 d φ d f \frac{d\varphi}{df} df d φ τ \tau τ
ただし、サンプリング定理を考慮すると TR = 2.5 sの場合、サンプリング制限は 0.2 Hz です。これは、コヒーレンス解析で着目する 0.1 - 0.2 Hz と近いため、これ以上 TR を長くするのは位相の推定に悪影響となります 。
また、時間遅れ τ \tau τ 。さらに、時間遅れ τ \tau τ N 1 ( t ) ≠ N 2 ( t − τ ) N_1(t) \ne N_2(t - \tau) N 1 ( t ) = N 2 ( t − τ )
Reference
Ashby, F. G. (2019). Statistical analysis of fMRI data. MIT press. url
相関とスペクトル解析 url
スペクトル解析 url
Sun, F. T., Miller, L. M., & D'Esposito, M. (2004). Measuring interregional functional connectivity using coherence and partial coherence analyses of fMRI data. Neuroimage, 21(2), 647-658. url