主成分分析(PCA)は、多変量統計手法の1つで、他の手法の前処理としてノイズや次元を削減するために使われています。
1. PCA
多変量正規分布に従うデータ [xi,yi] を考えます。
[xi,yi]∼N([μx,μy],[σx2covxycovxyσy2])
[xi,yi] に相関がある場合は、合わせて1つの指標として用いることが次元削減に繋がります。まずは、分散共分散行列を固有値分解します。
[σx2covxycovxyσy2]=[v1v2][d100d2][v1Tv2T]
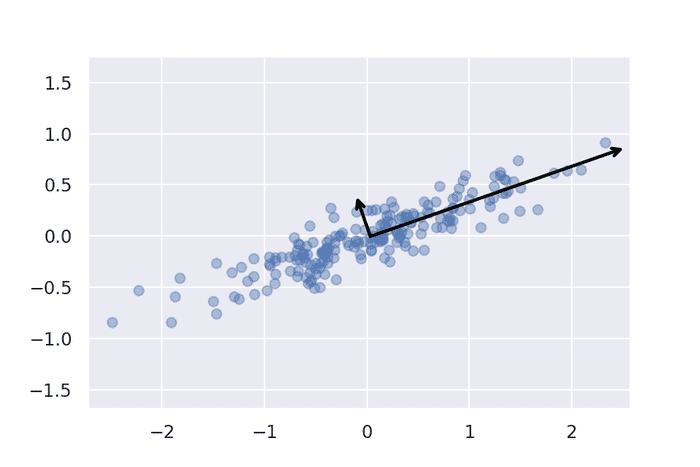
分散共分散行列は半正定値なので、固有値 d は正となります。固有ベクトル v は、データがつくる楕円形の等高線の軸に直交し、それら同士も直交します。固有ベクトル(主成分)の方向に新しい軸をとれば、多数の値を1つの軸で説明できるわけです。
固有値は、固有値ベクトルの方向における分散と一致します。ということは、各軸における情報量(寄与率)は、固有値に比例することになります。
第 r 主成分までの累積寄与率は、以下の式で求められます。これは、第 r 主成分までに説明しうる情報量の割合を示しています。
d1+d2+…+dnd1+d2+…+dr
2. fMRIデータへの適用
yj(i)が i 番目のTRの j 番目のボクセルにおける値だとします。PCAを適用するときは、各ボクセルの平均を0にした行列 YC を用います。
YC=⎣⎡y1(1)⋮y1(NTR)…⋱…yNv(1)⋮yNv(NTR)⎦⎤−⎣⎡1⋮1⎦⎤[yˉ1⋯yˉNv]
これを用いて、分散共分散行列 Σ∈RNv×Nv を推定できます。
Σ^=NTR−11YCTYC
Σ^ を固有値分解して固有ベクトルを算出し、その方向に射影します。Σ^ のランクは YCと一致するので、0ではない固有値 d は最大でTRの数 NTR だけあります。
Σ^=[v1⋯vNv]⎣⎡d1⋮0⋯⋱⋯0⋮dNv⎦⎤⎣⎡v1⊤⋮vNv⊤⎦⎤
zj(i)=yˉj+divij
タスクに敏感な信号は固有値が大きく、ノイズは固有値が小さくなると期待するわけです。
3. ノイズ除去
固有値が小さい要素を除くことで、ノイズを削減できます。
Yを正規化してYcsとし、分散共分散行列を計算し、固有値分解します。しかし、分散共分散行列 Σv=Ycs⊤Ycs∈RNv×Nv は大きいので、固有値を出すためなら
T=YcsYcs⊤=UDU⊤∈RNTR×NTR
と近似できます。最初の r 個を選択して Ur∈RNTR×r とし、これを用いて YC を射影します。
YC(r)=Ur⊤YC∈Rr×NTR
この YC(r) が、ノイズを削減した成分となります。
ボクセル空間に戻すには?
ノイズ削減後に元の空間に戻して、始めに引いた平均を加算してあげます。
Y^r=UrUr⊤YC+1yˉ⊤
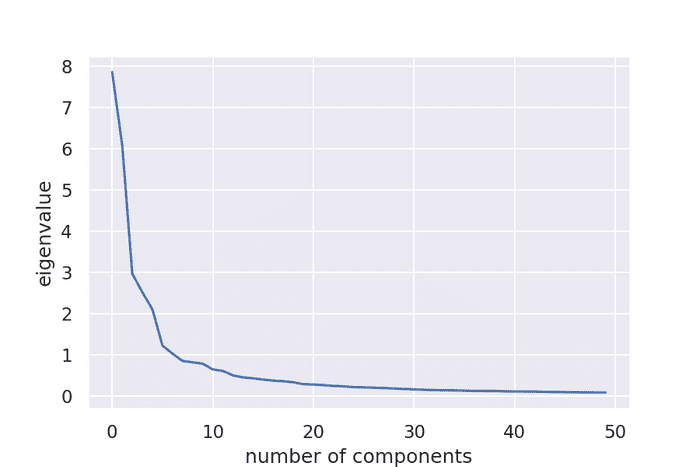
r の決め方
固有値を大きい順に並べて、Kinkと呼ばれる歪みの位置を基準にします(スクリープロット)。視覚的に見つからなければ、累積寄与率が90%となるようにします。
4. SVD
特異値分解 (SVD) がを使うと、分散共分散行列を直接必要としません。特異値分解は、次のように表されます。
YC=UGV⊤
ただし、U,Vは直交行列で、Gは対角行列と零行列を並べたものです。
このとき、Tは以下のように簡単に計算できます。
T =====YCsYCs⊤NTR−11YCYC⊤NTR−11(UGV⊤)(VG⊤U)NTR−11UGG⊤UU[NTR−11b2000]U⊤
SPMでは、SVDを適用して U から相関を取ってきているようです。
Reference
- Ashby, F. G. (2019). Statistical analysis of fMRI data. MIT press. url

