fMRI解析の基礎 (14)：動的因果モデリング

最終更新日: 2020年7月21日

fMRI解析の基礎シリーズ

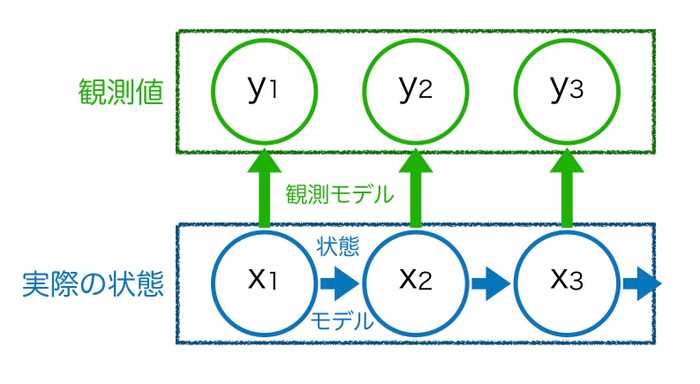
動的因果モデリング (Dynamic Causal Modeling, DCM) は、汎用的に使える、神経回路におけるコネクティビティを仮説検証する分析手法です (Friston et al. (2003))。

注目する脳領域を決め、その神経活動の経時変化をモデル化します。このモデルをデータに適合させると、脳領域同士の向きのある接続性が得られます。

状態空間モデルで、ブラックボックスの入力・出力をモデル化することを考えます。

入力 (input): $u(t)$
出力 (output): $x(t)$
入力係数 (input gain): $c$
自己フィードバック係数 (self-feedbuck gain): $a$

線形状態空間モデルでは、状態・観測モデルが線形に表現されます。

\text{state equation: } \frac{dx(t)}{dt}=a x(t) + c u(t)

脳神経をモデル化する場合は、 $a \lt 0$ とします。（leakey integrator）

\begin{array}{l} x(t) = e^{at} + K \\ \lim_{t \to \infty}x(t) = K = \text{Base Line} \end{array}

動的モデルを理解するために重要なのが、固定点です。

$u(t)=u$ で一定の場合、

x(t)=-\frac{c}{a}u

となり、入力が一定な間、出力は固定されます。

双線形システム：入力の係数が状態量の1次式になっている線形系

脳のシステムは、重ね合わせが成り立つような線形システムでないこともあります。DCMでは、双線形システムという比較的単純な非線形システムを用います。

ここで、脳領域１の入力を $u_1(t)$ 、出力を $x_1(t)$ とし、脳領域１の入力を $u_1(t)$ 、出力を $x_1(t)$ とするとき、以下の双線形動的モデルを考えます。

\begin{array}{rcl} \begin{pmatrix} \dot{x}_1(t) \\ \dot{x}_2(t)\end{pmatrix} & = & \begin{pmatrix} a_{11}& a_{12} \\ a_{21} & a_{22} \end{pmatrix} \begin{pmatrix} x_1(t) \\ x_2(t)\end{pmatrix} + u_1(t) \begin{pmatrix} b_{111}& b_{121} \\ b_{211} & b_{221} \end{pmatrix} \begin{pmatrix} x_1(t) \\ x_2(t)\end{pmatrix} \\[1em] & & + u_2(t) \begin{pmatrix} b_{112}& b_{122} \\ b_{212} & b_{222} \end{pmatrix} \begin{pmatrix} x_1(t) \\ x_2(t)\end{pmatrix} + \begin{pmatrix} c_{11}& c_{12} \\ c_{21} & c_{22} \end{pmatrix} \begin{pmatrix} u_1(t) \\ u_2(t)\end{pmatrix} \\[1em] \therefore \ \frac{dX}{dt} &=& (A+U^TB)X+CU \end{array}

双線形システムは、fMRI実験における神経活性化を、以下の手順に沿って直感的にモデル化できます。

ここで、 $A+U^TB$ の部分が脳領域同士の結合性を表現できることになります。

入力に制約を加えるとモデルの非線形性が低下し、実際の神経ダイナミクスを近似しづらくなってしまいます。そこで、より汎用的なDCMモデルが提案されています。

２次の非線形項を追加することで表現力を高めます。自由度が大幅に大きくなります。

\frac{dX}{dt}=(A+U^TB+X^TD)X+CU

各領域に２つの状態（興奮性・抑制性）のニューロン集団を仮定します。入力は興奮性 $E$ の出力のみとし、内的な働きは抑制性 $I$ の出力のみとします。

\begin{array}{rcl} \frac{dX}{dt} &= &JX+CU \\[0.5em] J_{ij}^{EE} &=& \mu_{ij}^{EE}\exp(A_{ij}^{EE}+\sum_k u_k B_{ij}^{EE(k)}) \\[0.5em] X &=& [x_1^E, x_1^I, \ \ldots, \ x_N^E,x_N^I] \end{array}

入力が定まらない安静時の接続性に使うことができます。誤差項を追加することで、領域間の時相関を考慮できます。

\frac{dX}{dt}=(A+U^TB)X+CU+E

$X$ をBOLD応答へ変換するために、HRFのモデルが必要となります。

一般的には、ベイズ推定を行います。以下のモデルを仮定します。

\begin{array}{l} y(t) = g[x(t), \theta]+\varepsilon(t) \\[0.5em] \varepsilon(t) \sim N(0,\sigma_{\varepsilon}^2) \end{array}

誤差の共分散構造は、相関を考慮するものと、独立と仮定するものがあります。独立と仮定した場合は、積の法則を用いることができます。

p[y(t_1),y(t_2),\cdots, y(t_{N_{TR}})|\theta] = \prod_{i=1}^{N_{TR}}p[y(t_i)|\theta]

このとき、最尤推定やMAP推定が簡単に行えます。事前分布 $p(\theta)$ には、経験的な分布を用います。

\begin{array}{l} \theta_{\text{ML}} = \max_{\theta} \ p(y_1,y_2,\ldots,y_N|\theta) \\ \theta_{\text{MAP}} = \max_{\theta} \ p(y_1,y_2,\ldots,y_N|\theta) p(\theta) \end{array}

DCMでは、いくつかのネットワーク構造を比較できます。「最適性」を定義するのは難しく、適合度とモデルの簡潔さとのトレードオフとなります。着目する領域は揃えたほうがよく、少数に絞って組み合わせ爆発しないようにします。

ベイズ推定では、モデルエビデンスを最大化してモデルを選択する方法があります。

p(Y|M_i)=\int p(\theta|M_i)p(Y|M_i,\theta)d\theta

モデルエビデンスの定量化には、ベイズ因子が利用できます¹。ただし、この計算は複雑で負荷が大きいです。

BF_{ij}=\frac{p(Y|M_i)}{p(Y|M_j)}

ベイズ情報量基準 (BIC) は、ラプラス近似（事後分布をガウス分布で近似）における自由エネルギーの、サンプルサイズが無限大の漸近挙動を単純化したものです²。

BIC(M_i) = -2 \log p(Y|M_i, \hat{\theta}) + d \log n

エビデンス下界 ELBO (Evidence Lower Bound) を最大化します³。ここでは、KLダイバージェンスを用いてELBOを設計しています。

\mathrm{ELBO(M_i)} = \int q(\theta,M_i) \log \frac{p(Y,\theta)}{q(\theta,M_i)}

Ashby, F. G. (2019). Statistical analysis of fMRI data. MIT press. url
Friston, K. J., Harrison, L., & Penny, W. (2003). Dynamic causal modelling. Neuroimage, 19(4), 1273-1302. url