fMRI解析の基礎 (11)：独立成分分析

**ICA（独立成分分析）**は、PCAよりも強力で、現実的な潜在構造に基づいています。多くのパラメータを持っていて複雑なモデルを設計できる上に、正規性の仮定が無いという利点があります。

１. カクテルパーティー問題

カクテルパーティー問題と呼ばれる複数の音声の分離問題に、ICAを適用できます。

異なる話者の音声波形は互いに独立であるため、重ね合わせによってできている音源から各音声波形を分離できるのです。各音声波形に対してそれぞれ重みがあるとすれば、その重みを推定してあげればよいのです。

２. fMRIデータへの適用

ICAには、Temporal ICA と Spatial ICA があります。fMRIデータに適用されるのは Spacial ICA であり、次元の高いボクセル空間での次元削減が行われます。

• Temporal ICA : 時系列方向の独立成分分析
  • 各ボクセルに重みがある。
• Spatial ICA : 立体空間方向の独立成分分析
  • 各TRに重みがある。

Spatial ICA では、各成分 $c_k$ を線形結合した信号をBOLD信号として考えます。各TRの信号 $y^{(t)}$ について考えると、成分 $c_k$ だけが共通となります。

制約を与えないと解が一意に定まらないので、各成分は独立でそれぞれの分散が$1$とします。$M$ が正則ならば逆行列を用いて $C$ を求められます。

ICAを行うアルゴリズムはたくさんあり、$C$ に着目するものや、 $M$ の逆行列 $U$ に着目するものなどがあります。

統計的独立性の評価

系列 $x$ と 系列 $y$ が統計的に独立なときは、すべての $x,y$ において $p(x,y)=p(x)p(y)$ が成立します。しかし、これを確認する理想的な方法はありません 。

ピアソンの相関係数が代替として挙げられますが、１次と２次の統計量にしか依存していないため、高次の相関関係に弱くなります。

非正規分布

正規分布より「高いピーク」「高い尾」を持っている確率分布を考えます（leptokurtic distribution や super-Gaussian と呼ばれます）。例えば、下図のラプラス分布があります。

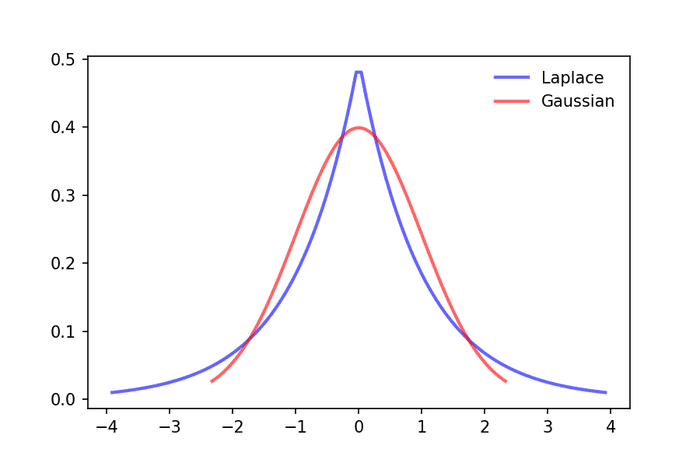
このような非正規分布はfMRIデータにうまく適合することが知られています。ほとんどのボクセルはタスクに対して応答が0である一方、一部のボクセルはかなり大きい応答を示すことをよく説明できるからです。

ICAの事前準備

1. Mean Centering：時間方向で平均を$0$にし、ボクセル方向で平均を$0$にする。（順不同）
2. Whitening：分散共分散行列を、分散$1$・共分散$0$にする。（$D^{-\frac{1}{2}}V^T$や$A^{-1}$で変換）

３. ICAのアルゴリズム

ICAのアルゴリズムは多く提案されています。基本的には、成分 $c_k$ どうしが独立になることを目指します。

A. 相互情報量の最小化

エントロピー $H$ を用いて、相互情報量 $I$ を規定します。

相互情報量は、「$X$ を観測したときに $Y$ の情報がどのくらい増えるか？」を示しているため、$I(X,Y)=0$ のときに $X$ と $Y$ は独立であるといえます。

ICAに適用する方法の一つは、独立成分 $C$ の行同士の相互情報量を最小にするように $U$ を選択する方法です。これには、高次のモーメントの誤差が大きいという欠点があります。

B. 非正規性の最大化

1. 尖度 (Kurtosis) の最大化
   • 分布のピークを最大化する。外れ値に弱い。
2. ネゲントロピー (Negentropy) の最大化
   • 正規分布からどれくらい外れているかの指標であるネゲントロピー $J(X)$ を最大化する。これが$0$だと$X$は正規分布に従う。

ネゲントロピーは相互情報量より推定が難しいです。そのため、３次と４次のモーメントを多項式の期待値で近似した方法（Hyvarinrn (1999)）が、FastICAとして広く使われています。

C. 最尤法

いくつかの条件¹を満たす場合に以下の尤度関数が得られます。

$f(c_{kj})$ はボクセル $j$ 、成分 $k$ の尤度であり、super-Gaussian を用います。

D. 情報量最大化原理 Infomax principle

ニューラルネットで使われる情報量の最大化を考えます。入力 $y$ に、 $U$ に相当する線形変換をし、活性化関数 $g$ ² を通した出力 $a$ を得るとします。この出力同士の結合情報量 $H(a_i,a_j)$ を最大化することで、出力をできるだけ均等に分布させます。これにより、成分の統計的独立性が最大化されます。

活性化関数には super-Gaussian を用いた方がよいとされます。その非線形性により、ただ単に $U$ の情報量を最大化する以上のことができると考えられます。

４. ICAの解釈

ICAを解釈する時には、次のような問題があります。

1. 成分の重要度が直接得られない。
2. 成分ごとに要因を考える必要がある。

重要度の比較

最も単純なのは、ある成分を零ベクトルにしたときの変動（二乗誤差）を比べる方法です。

要因の考察

自動化は困難なので³、明白な成分だけを考慮します。成分の重みと空間マップを利用して要因を決定します。

タスクが要因のものは、タスク呈示との関連を考慮します。生理学的ノイズが要因のものは、位置（頭蓋骨近く＝頭部動き由来）や周期性（呼吸・心拍）などを考慮します。

５. Noisy ICA

ノイズ $\varepsilon_{V(i)}$ を考慮したモデルは上のようになります。

このとき、 $U$ を求めるのは通常のICAより困難です。

また、ノイズの分散共分散行列 $\Sigma_i$ が未知であることも問題となります。FSLでは、$\Sigma_i=\sigma^2I$ と仮定しているようです。

Noisy ICA の利点は、統計学的根拠が明確であることです。独立成分の確率分布から要因の議論ができます。

６. 諸問題

• Mが正方行列であることで計算が楽になるので、そんなに無いとしても$N_{TR}$の独立成分を全部推定するほうが良い。
• ただ、FastICAでは独立成分が少ないほうが計算時間を減らせる。
• ICAの前にPCAでノイズ除去するのは共線性を高めて良くないこともある。PCA→FastICAは良い。

７. Group ICA

一般的に使われるGroup ICA では、複数の被験者を時間軸で連結して１つの ICA をします。PCAでノイズ除去してから ICA をかけます。

タスクとの時系列相関から、被験者間に共通なタスク応答ネットワークを統計的有意性で議論できます。また、StatMapを作ることもできます。

８. ICA 対 GLM

---

Reference

• Ashby, F. G. (2019). Statistical analysis of fMRI data. MIT press. url
• Hyvarinen, A. (1999). Fast and robust fixed-point algorithms for independent component analysis. IEEE transactions on Neural Networks, 10(3), 626-634. url