サポートベクトルマシンとサポートテンソルマシン：SVM・STM

最終更新日: 2020年6月18日

サポートベクトルマシン（Support Vector Machine）とは？

サポートベクトルマシンとは、分類の基準を決める際に基準に近いデータのみを利用するような分類器です。

この分類器では、モデルの複雑さを最小化できます。言い換えれば、バリアンスを最小化できるということです。また、外れ値にも強いロバストな分類器であるともいえます。

サポートベクトルマシンでは、マージン（Margin） という概念が重要です。下図においてマージンは、超平面（基準）とサポートベクトルとの最大幅を指します。マージンを最大にするような超平面（基準）は、２つのクラスを最適に分けると考えられるでしょう。

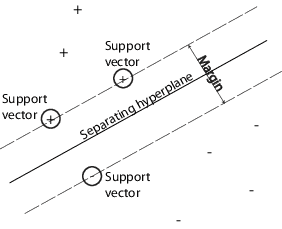
サポートベクトルマシンの分類（Mathworks documentation より引用 link)

マージン内に違反（クラス1側にクラス2の点が存在するなど）を許容しないマージンを ハードマージン、許容するマージンをソフトマージンといいます。一般的には、線形分離不可能な（平面で完全に分けられない）データに対応するために、ソフトマージンを使用します。

サポートベクトルマシン（Support Vector Machine）の定式化

分類したいデータセット $D$ を、Ｍ個のデータ $\boldsymbol{x}_i \in \R^n$ とラベル $y_i \in \{-1, 1\}$ から成ることとします。このとき、データの線形和とバイアス $b$ によって定める超平面 $f(\boldsymbol{x})$ によって分類しましょう。

D=\{\boldsymbol{x}_i, y_i\}_{i=1}^{M} \\ f(\boldsymbol{x}) = \boldsymbol{w}^T \boldsymbol{x} + b

このとき、ソフトマージン最大化は以下の最適化問題に帰着します。

\min_{\boldsymbol{w},b,\xi} \ \frac{1}{2}\|\boldsymbol{w}\|^2 + C\sum_{i=1}^M \xi_i \\ \mathrm{subject \ to} \left\{ \begin{array}{l} y_i(\boldsymbol{w}^T \boldsymbol{x} + b) \ge 1 - \xi_i \\ \forall i: \xi_i \ge 0 \end{array} \right.

ここで、式を簡素にするためにスラック変数 $\xi_i$ を導入しました。定数 $C$ は、マージン内の違反をどれだけ許容するかを決めます。つまり、 $C=0$ の場合がハードマージンとなります。

この問題は「制約付き最適化問題」なので、ラグランジュの未定乗数法とKKT条件を用いて以下の双対問題に書き換えることができます。

\max_{\alpha_1, \dots, \alpha_M} \sum_{i=1}^{M} \alpha_i - \frac{1}{2} \sum_{i=1}^{M} \sum_{j=1}^{M} \alpha_i \alpha_j y_i y_j \langle \boldsymbol{x}_i, \boldsymbol{x}_j \rangle \\ \mathrm{subject \ to} \left\{ \begin{array}{l} \sum_{i=1}^{M}\alpha_i y_i = 0 \\ \forall i: 0 \le \alpha_i \le C \end{array} \right.

ここで、 $\langle \boldsymbol{x}_i, \boldsymbol{x}_j \rangle$ は２つのベクトルの内積を示しています。書き換えによって、最適化すべき変数はラグランジュ変数 $\alpha_i$ のみとなりました。後はこの最適化問題を凸二次計画法で解くことになります。このとき $\alpha_i=0$ となったサンプルは、重みも0になるため使われません。そのため、 $\alpha_i\gt0$ となったサンプルだけがサポートベクトルとして使われるわけです。

参考：統計数理研究所公開講座４．サポートベクターマシン

カーネルトリック

データセットが線形分離不可能な場合、非線形な超平面で分離したいと考えるでしょう。このとき、超平面 $f(\boldsymbol{x})$ は非線形関数 $\phi (\boldsymbol{x})$ を用いて以下のように表すことができます。

f(\boldsymbol{x}) = \boldsymbol{w}^T \phi (\boldsymbol{x}) + b

このとき、最適化問題の双対問題は同じように定式化できます。

\max_{\alpha_1, \dots, \alpha_M} \sum_{i=1}^{M} \alpha_i - \frac{1}{2} \sum_{i=1}^{M} \sum_{j=1}^{M} \alpha_i \alpha_j y_i y_j \langle \phi (\boldsymbol{x}_i), \phi (\boldsymbol{x}_j) \rangle \\ \mathrm{subject \ to} \left\{ \begin{array}{l} \sum_{i=1}^{M}\alpha_i y_i = 0 \\ \forall i: 0 \le \alpha_i \le C \end{array} \right.

ここで、 $\langle \phi (\boldsymbol{x}_i), \phi (\boldsymbol{x}_j) \rangle = k(\boldsymbol{x}_i, \boldsymbol{x}_j)$ のようにカーネル関数 $k(\cdot \ , \cdot)$ で置き換えてしまうことで、 $\phi (\boldsymbol{x})$ を明示的に計算する必要が無くなります。この置き換えをカーネルトリックといいます。

カーネル関数には、多項式カーネル・ガウスカーネル・シグモイドカーネルなどがよく用いられます。カーネル関数は Mercer の定理を満たしていれば、高次元の内積空間を計量できることが示されています。

参考：カーネルトリック

サポートテンソルマシン（Support Tensor Machine）とは？

サポートテンソルマシンとは、ベクトルしか扱えなかったサポートベクトルマシンをテンソルを扱えるように拡張した分類器です。

テンソルは身近な構造的データに度々現れます。例えば、縦・横・奥行きのMRI画像は３次元のテンソル＝ 3-order Tensor となります。カラー画像も、RGBと縦・横の軸があり、 $3 \times$ 縦 $\times$ 横の３次元のテンソル＝ 3-order Tensor となります。

テンソルとベクトルの演算方法のひとつ Tensor k-mode product を導入します。

Tensor k-mode product

kモード（k番目の軸）に対してベクトルの内積を取るような演算です。テンソルの縮約とも呼ばれます。

例として、３次元のテンソル $\mathcal{X} \in \R^{N_1 \times N_2 \times N_3}$ にベクトル（２次元のテンソル） $\boldsymbol{a} \in \R^{P \times N_k}$ を掛けることを考えます。このとき、Tensor k-mode product $\mathcal{X}' = \mathcal{X} \times_k \boldsymbol{a}$ は要素ごとに見ると以下のようになります。

k = 1 : \mathcal{X}'_{p, n_2, n_3} = \sum_{\bold{n}=1}^{N_1} \mathcal{X}_{\bold{n}, n_2, n_3} \boldsymbol{a}_{p\bold{n}} \ \ \ \ ( \mathcal{X}'\in \R^{P \times N_2 \times N_3} ) \\ k = 2 : \mathcal{X}'_{n_1, p, n_3} = \sum_{\bold{n}=1}^{N_2} \mathcal{X}_{n_1, \bold{n}, n_3} \boldsymbol{a}_{p\bold{n}} \ \ \ \ ( \mathcal{X}'\in \R^{N_1 \times P \times N_3} ) \\ k = 3 : \mathcal{X}'_{n_1, n_2, p} = \sum_{\bold{n}=1}^{N_3} \mathcal{X}_{n_1, n_2, \bold{n}} \boldsymbol{a}_{p\bold{n}} \ \ \ \ ( \mathcal{X}'\in \R^{N_1 \times N_2 \times P} )

k番目の要素を積和に置き換えるような演算です。演算後のテンソルが変形しているのに気をつけてください。

サポートテンソルマシン（Support Tensor Machine）の定式化

３次元のテンソル $\mathcal{X} \in \R^{N_1 \times N_2 \times N_3}$ とラベル $y_i \in \{-1, 1\}$ から成るデータセット $D = \{\mathcal{X}_i, y_i\}_{i=1}^{M}$ を、超平面 $f(\mathcal{X})$ で分類しましょう。分類平面は、以下のような式で表します。

f(\mathcal{X}) = \mathcal{X} \times_1 \boldsymbol{w}^{(1)} \times_2 \boldsymbol{w}^{(2)} \times_3 \boldsymbol{w}^{(3)} + b \\ \mathrm{where} \ \ \boldsymbol{w}^{(1)} \in \R^{1 \times N_1}, \ \boldsymbol{w}^{(2)} \in \R^{1 \times N_2}, \ \boldsymbol{w}^{(3)} \in \R^{1 \times N_3}

ここで、 $\hat{y} = f(\mathcal{X})$ は Tensor k-mode product によって $\hat{y} \in \R^{1 \times 1 \times 1}$ となります。つまり、要素は１つになるわけです。

さて、この重みを最適化するためにはどうしたらよいでしょうか。ここでは、交互射影法を用いて１つずつ重み $\boldsymbol{w}^{(k)}$ を最適化します。各重み $\boldsymbol{w}^{(k)}$ に対する最適化問題は以下となります。

\min_{\boldsymbol{w}^{(k)},b,\xi} \ \frac{1}{2} \beta \|\boldsymbol{w}^{(k)}\|^2 + C\sum_{i=1}^M \xi_i \\ \mathrm{subject \ to} \left\{ \begin{array}{l} y_i((\boldsymbol{w}^{(k)})^T \hat{\boldsymbol{x}}_i + b) \ge 1 - \xi_i \\ \forall i: \xi_i \ge 0 \\ \end{array} \right.

ここで、 $\beta=\prod_{1\le l \le3}^{l \ne k} \|\boldsymbol{w}^{(l)}\|$ かつ $\hat{\boldsymbol{x}}_i = \mathcal{X}_i \prod_{1\le l \le3}^{l \ne k} \times_l \ \boldsymbol{w}^{(l)}$ としました。これは、通常のサポートベクトルマシンの主問題と同じ形式であるため、同様に双対問題に変形できます。

\max_{\alpha_1, \dots, \alpha_M} \sum_{i=1}^{M} \alpha_i - \frac{1}{2} \beta \sum_{i=1}^{M} \sum_{j=1}^{M} \alpha_i \alpha_j y_i y_j \langle \hat{\boldsymbol{x}}_i, \hat{\boldsymbol{x}}_j \rangle \\ \mathrm{subject \ to} \left\{ \begin{array}{l} \sum_{i=1}^{M}\alpha_i y_i = 0 \\ \forall i: 0 \le \alpha_i \le C \end{array} \right.

初期化した重みを順次更新して、損失が収束するまで繰り返すことで全ての重みを最適化できます。

※今回は３次元のテンソルについて書きましたが、このまま容易にＮ次元のテンソルに拡張できます。

サポートテンソルマシン（Support Tensor Machine）の特徴

利点：最適化するパラメータが少ないため、過剰適合しにくい。
欠点：テンソルの縮約によりランク1の表現となるため、表現力が低い。

Reference

Support Vector Machines - scikit-learn https://scikit-learn.org/stable/modules/svm.html
バイナリ分類のサポートベクターマシン - MathWorks link
統計数理研究所公開講座４．サポートベクターマシン pdf
Dacheng Tao, Xuelong Li, Weiming Hu, Maybank, S., Xindong Wu, 2005. Supervised tensor learning, Presented at the Fifth IEEE International Conference on Data Mining (ICDM’05), pp. 8 pp.-. https://doi.org/10.1109/ICDM.2005.139
Chen, C., Batselier, K., Ko, C.-Y., Wong, N., 2018. A Support Tensor Train Machine. arXiv:1804.06114 https://arxiv.org/abs/1804.06114