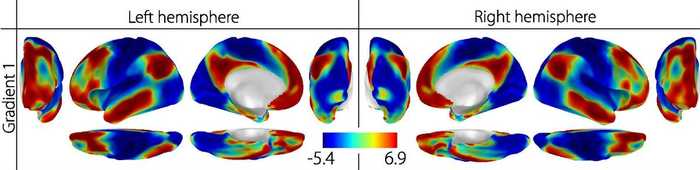
安静時fMRIにおける勾配
上図の安静時fMRIの解析結果においては、赤から青にかけての階層性 が表現されています。この階層性は、勾配 を用いて定量的に計算することができます。では、この勾配とはなんなのでしょうか?
勾配とは?
勾配 (Gradients) : 脳のマクロな特徴を低次元多様体に写像したもの
類似度行列の計算
…領域間における特徴量の類似性 を捉えます。
2. 低次元への変換 埋め込み を行います。
3. 階層性の特定 階層性 を特定します。
勾配の計算方法:機能的結合性の例
勾配を用いると、「脳内処理が統合することで脳機能にどのような影響があるか」を理解することができます 。例えば、皮質全体の勾配パターンとダイナミクス・高次認知との関係、勾配の摂動と精神疾患との関係、脳構造と機能的測定との関係などが示されています
勾配の計算方法
Wawl et al. (2020) を参考に、解析の一例をまとめました。使用しているデータは、HCP (Human Connectome Project) の安静時fMRIのデータです。
類似度行列の計算
入力 X = ( x 1 , ⋯ , x n ) ⊤ X = (\bold{x}_1, \cdots, \bold{x}_n)^{\top} X = ( x 1 , ⋯ , x n ) ⊤ A ∈ R n × n A \in \R^{n \times n} A ∈ R n × n
各 x i , x j \bold{x}_i, \bold{x}_j x i , x j
ガウシアンカーネル (Gaussian kernel)
γ \gamma γ ∥ ⋅ ∥ 2 \| \cdot \|_2 ∥ ⋅ ∥ 2
A i j = exp ( − γ ∥ x i − x j ∥ 2 ) A_{ij} = \exp (-\gamma \| \bold{x}_i - \bold{x}_j \|^2) A ij = exp ( − γ ∥ x i − x j ∥ 2 )
コサイン類似度 (Cosine similarity)
A i j = x i x j ⊤ ∥ x i ∥ ∥ x j ∥ A_{ij} = \frac{\bold{x}_i \bold{x}_j^{\top}}{\| \bold{x}_i \| \| \bold{x}_j \|} A ij = ∥ x i ∥∥ x j ∥ x i x j ⊤
正規化コサイン類似度 (Normalized angle similarity)
A i j = 1 − 1 π cos − 1 ( x i x j ⊤ ∥ x i ∥ ∥ x j ∥ ) A_{ij} = 1- \frac{1}{\pi} \cos^{-1} \left( \frac{\bold{x}_i \bold{x}_j^{\top}}{\| \bold{x}_i \| \| \bold{x}_j \|} \right) A ij = 1 − π 1 cos − 1 ( ∥ x i ∥∥ x j ∥ x i x j ⊤ )
ピアソンの相関係数 (Pearson correlation)
A i j = ( x i − x ˉ i ) ( x j − x ˉ j ) ⊤ ∥ x i − x ˉ i ∥ ∥ x j − x ˉ j ∥ A_{ij} = \frac{(\bold{x}_i - \bar{\bold{x}}_i) (\bold{x}_j - \bar{\bold{x}}_j)^{\top}}{\| \bold{x}_i - \bar{\bold{x}}_i \| \| \bold{x}_j - \bar{\bold{x}}_j \|} A ij = ∥ x i − x ˉ i ∥∥ x j − x ˉ j ∥ ( x i − x ˉ i ) ( x j − x ˉ j ) ⊤
スピアマンの順位相関係数 (Spearman rank order correlation)
r i \bold{r}_i r i x i \bold{x}_i x i
A i j = ( r i − r ˉ i ) ( r j − r ˉ j ) ⊤ ∥ r i − r ˉ i ∥ ∥ r j − r ˉ j ∥ A_{ij} = \frac{(\bold{r}_i - \bar{\bold{r}}_i) (\bold{r}_j - \bar{\bold{r}}_j)^{\top}}{\| \bold{r}_i - \bar{\bold{r}}_i \| \| \bold{r}_j - \bar{\bold{r}}_j \|} A ij = ∥ r i − r ˉ i ∥∥ r j − r ˉ j ∥ ( r i − r ˉ i ) ( r j − r ˉ j ) ⊤ 今回の例では、コサイン類似度 を計算しています。
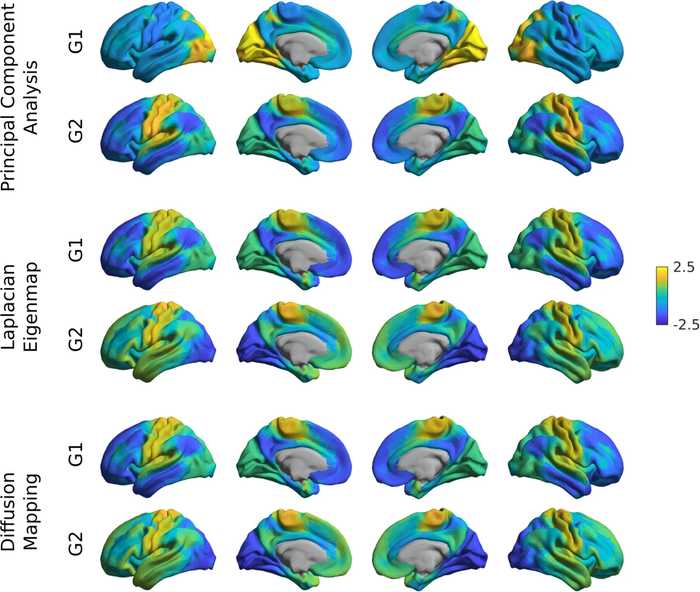
低次元への変換(次元削減)
類似度行列 A A A m m m G ∈ R n × m \mathcal{G} \in \R^{n \times m} G ∈ R n × m
変換方法には以下のようなものがあります。
主成分分析では、線形変換をしていくつかの直交基底からなる空間に写像します 。特異値分解をして求めた U , S U, S U , S
A = U S V ⊤ G PCA = U S ⊤ A = USV^{\top} \\
\mathcal{G}_{\text{PCA}} = US^{\top} A = U S V ⊤ G PCA = U S ⊤
ラプラス固有写像 (Laplacian Eigenmaps)
ラプラス固有写像では、グラフラプラシアン L = D − A L = D - A L = D − A 。ここで、D D D A A A D i i = ∑ j A i j D_{ii} = \sum_j A_{ij} D ii = ∑ j A ij m m m { g 1 , ⋯ , g m } \{\bold{g}_1, \cdots, \bold{g}_m \} { g 1 , ⋯ , g m }
L g k = λ k D g k G LE = ( g 1 , ⋯ , g m ) ⊤ L\bold{g}_k = \lambda_k D \bold{g}_k \\
\mathcal{G}_{\text{LE}} = (\bold{g}_1, \cdots, \bold{g}_m)^{\top} L g k = λ k D g k G LE = ( g 1 , ⋯ , g m ) ⊤
拡散マップ (Diffusion Mapping)
拡散マップでは、遷移行列 P α = D α − 1 W α P_\alpha = D_\alpha^{-1} W_\alpha P α = D α − 1 W α 。ここで、α \alpha α W α = D − 1 / α A D − 1 / α W_\alpha=D^{-1/\alpha}AD^{-1/\alpha} W α = D − 1/ α A D − 1/ α W α W_\alpha W α D α D_\alpha D α m m m
P α g k = λ k D g k G DM = ( λ 1 ⊤ g 1 , ⋯ , λ m ⊤ g m ) ⊤ P_\alpha\bold{g}_k = \lambda_k D \bold{g}_k \\
\mathcal{G}_{\text{DM}} = (\lambda_1^{\top}\bold{g}_1, \cdots, \lambda_m^{\top} \bold{g}_m)^{\top} P α g k = λ k D g k G DM = ( λ 1 ⊤ g 1 , ⋯ , λ m ⊤ g m ) ⊤ これら3つの方法で取得した低次元表現 G \mathcal{G} G
機能的結合性の勾配
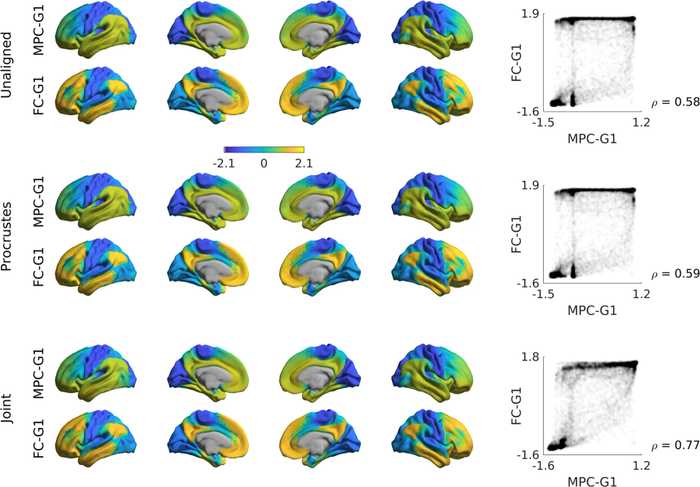
勾配を揃える
複数のデータセットや被験者間などで勾配を比較するとき、固有ベクトルの不一致が発生する可能性があります。そのため、比較のために勾配を揃える必要があります 。
プロクラステス解析 (Procrustes Analysis)
プロクラステス解析では、直行線形変換 ψ \psi ψ G R \mathcal{G}_R G R { G k } \{ \mathcal{G}_k \} { G k }
(1) Choose the first reference G R . (2) Align. G R − ψ ( G k ) ∼ 0 (3) Update. G R = 1 N ∑ k ψ ( G k ) (4) Iterate (2) - (4). \begin{array}{rl}
\text{(1)} & \text{Choose the first reference } \mathcal{G}_R . \\
\text{(2)} & \text{Align. } \ \mathcal{G}_R - \psi(\mathcal{G}_k) \sim 0 \\
\text{(3)} & \text{Update. } \ \mathcal{G}_R = \frac{1}{N} \sum_k \psi(\mathcal{G}_k)\\
\text{(4)} & \text{Iterate (2) - (4). }
\end{array} (1) (2) (3) (4) Choose the first reference G R . Align. G R − ψ ( G k ) ∼ 0 Update. G R = N 1 ∑ k ψ ( G k ) Iterate (2) - (4). 結合埋め込みでは、複数の表現の共通表現を見つけるために、結合類似度行列 J \mathcal{J} J k k k X k X_k X k A k A_k A k X k X_k X k A k l A_{kl} A k l X k , X l X_k, X_l X k , X l J \mathcal{J} J G J \mathcal{G}_J G J
J = ( A 1 A 12 … A 1 N A 12 ⊤ A 22 … A 2 N ⋮ ⋮ ⋱ ⋮ A 1 N ⊤ A 2 N ⊤ … A N ) G J = ( G 1 , ⋯ , G N ) ⊤ \mathcal{J} =
\left(
\begin{array}{cccc}
A_{ 1 } & A_{ 12 } & \ldots & A_{ 1N } \\
A_{ 12 }^{\top} & A_{ 22 } & \ldots & A_{ 2N } \\
\vdots & \vdots & \ddots & \vdots \\
A_{ 1N }^{\top} & A_{ 2N }^{\top} & \ldots & A_{ N }
\end{array}
\right) \\ \ \\
\mathcal{G}_J = (\mathcal{G}_1, \cdots, \mathcal{G}_N)^{\top} J = ⎝ ⎛ A 1 A 12 ⊤ ⋮ A 1 N ⊤ A 12 A 22 ⋮ A 2 N ⊤ … … ⋱ … A 1 N A 2 N ⋮ A N ⎠ ⎞ G J = ( G 1 , ⋯ , G N ) ⊤ これら2つの方法で揃えた勾配は、下図のようになります。
勾配の重ね合わせ
帰無仮説検定
他のモダリティとの相関を評価する差異、空間的な自己相関によるバイアスが大きくなることが予想されます。これを回避するために順列検定を行い、類似した空間的自己相関をもつ分布との相関と比較することが重要です 。
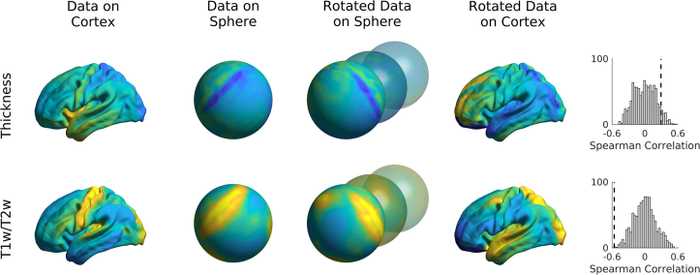
スピン順列検定 (Spin Permutations)
スピン順列検定では、皮質の球体表現を活用します。球面上の座標 V l ∈ R l × 3 V_l \in \R^{l \times 3} V l ∈ R l × 3 R ∈ R 3 × 3 R \in \R^{3 \times 3} R ∈ R 3 × 3
Moran Spectral Randomization
MSRを用いて、類似の空間的な自己相関をもった確率変数を生成することもできます
スピン順列検定を用いて 皮質厚や T1w/T2w 画像と比較した例が下図です。T1w/T2w 画像のみに有意な相関がみられたようです。
スピン順列検定
次回は、勾配解析を実際にPythonで行ってみたいと思います。
→ Pythonで脳の勾配を計算する - BrainSpace
Reference
Margulies, D. S., Ghosh, S. S., Goulas, A., Falkiewicz, M., Huntenburg, J. M., Langs, G., ... & Jefferies, E. (2016). Situating the default-mode network along a principal gradient of macroscale cortical organization. Proceedings of the National Academy of Sciences, 113(44), 12574-12579. url
de Wael, R. V., Benkarim, O., Paquola, C., Lariviere, S., Royer, J., Tavakol, S., ... & Misic, B. (2020). BrainSpace: a toolbox for the analysis of macroscale gradients in neuroimaging and connectomics datasets. Communications biology, 3(1), 1-10. url