PythonでResting-state fMRIの結合性解析 - Nilearn

最終更新日: 2020年9月30日

Jupyter Notebookはこちら

NilearnはfMRIデータなどの扱いや統計的学習に特化したPythonパッケージです。

Nilearn is a Python module for fast and easy statistical learning on NeuroImaging data. - Nilearn

Nilearnを利用して次のようなことができます。

データセットの取得
MRI画像の読み込み・処理
マスクの利用
Surfaceデータの利用
デコーディングや独立成分分析
結合性解析
高度な視覚化

また、種々のクラスやメソッドが scikit-learn like になっています。

ここでは

を参考に結合性解析とネットワーク解析を行っていきます。

Nilearn のインストール

pipでインストールできます。

pip install nilearn

参考：Installing nilearn

rsfMRIデータとアトラスデータの取得

まず、アトラスデータをダウンロードします。

ここでは、Dosenbach et al. のアトラスを利用しました。領域（ROI）ごとに座標・領域名・ネットワーク名があります。

Python

from nilearn import datasets, image

# Load the atlas dataset
atlas = datasets.fetch_coords_dosenbach_2010()
coordinates = atlas['rois']
labels = atlas['labels']
networks = atlas['networks']

for coord,label,network in zip(coordinates[:3],labels[:3],networks[:3]):
    print("coord:{}, label: {}, network: {}".format(coord,label,network))

Output

coord:(18, -81, -33), label: b'inf cerebellum' 155, network: b'cerebellum'
coord:(-21, -79, -33), label: b'inf cerebellum' 150, network: b'cerebellum'
coord:(-6, -79, -33), label: b'inf cerebellum' 151, network: b'cerebellum'

次に、Resting-state fMRI (rsfMRI) データをダウンロードします。

ここでは、ABIDE¹のrsfMRIデータを利用しました。1人分のデータを取得します。

4D画像のサイズは (61, 73, 61, 196) です。（つまり 196 TRs）

Python

# Load the resting-state functional dataset
data = datasets.fetch_abide_pcp(n_subjects=1)
print("the shape of 4D Image:", image.load_img(data.func_preproc[0]).shape)
print("the zoom of 4D Image:", image.load_img(data.func_preproc[0]).header.get_zooms())

Output

the shape of 4D Image: (61, 73, 61, 196)
the zoom of 4D Image: (3.0, 3.0, 3.0, 1.5)

領域の信号を抽出する

rs-fMRIデータのボクセル $61 \times 73 \times 61 \sim 270,000$ 個同士の相関を考えるのではなく、160個の領域（ROI）同士の相関を考えることにします。そのために、各領域の信号を抽出します。

今回はアトラスが座標データなので、その座標を中心とした球体を領域として信号を抽出します。

Python

from nilearn import input_data 

masker = input_data.NiftiSpheresMasker(seeds=coordinates, radius=4.5,
                                        detrend=True, standardize=True,
                                        low_pass=0.1, high_pass=0.01, t_r=1.5,
                                        memory='nilearn_cache', memory_level=1)

time_series = masker.fit_transform(data.func_preproc[0])
print("the shape of time series:", time_series.shape)

Output

the shape of time series: (196, 160)

196 TRs $\times$ 160 ROIs の時系列データが抽出されました。

例として2つの領域の信号を見てみましょう。

Python

import matplotlib.pyplot as plt

f = plt.figure(dpi=100)
plt.plot(time_series[:,0], label=labels[0])
plt.plot(time_series[:,1], label=labels[1])
plt.xlabel("TRs"); plt.ylabel("Intensity")
plt.legend(); plt.show()

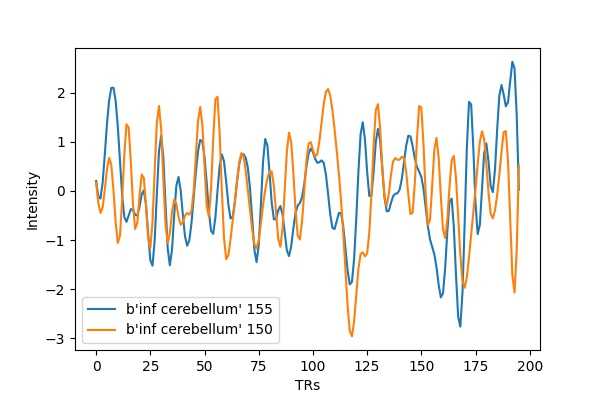
相関行列を計算する

時系列データの相関行列を計算して描画します。これが領域同士の結合性となります。

今回は "correlation" を計算しました。{"correlation", "partial correlation", "tangent", "covariance", "precision"} の中から選ぶことができます。

Python

import numpy as np
from nilearn import connectome, plotting

# Build the correlation matrix
correlation_measure = connectome.ConnectivityMeasure(kind='correlation')
correlation_matrix = correlation_measure.fit_transform([time_series])[0]

# Display the correlation matrix
np.fill_diagonal(correlation_matrix, 0)
plotting.plot_matrix(correlation_matrix, colorbar=True)
plt.title("Correlation matrix"); plt.xlabel("ROIs"); plt.ylabel("ROIs")
plt.xticks([]); plt.yticks([]); plt.show()

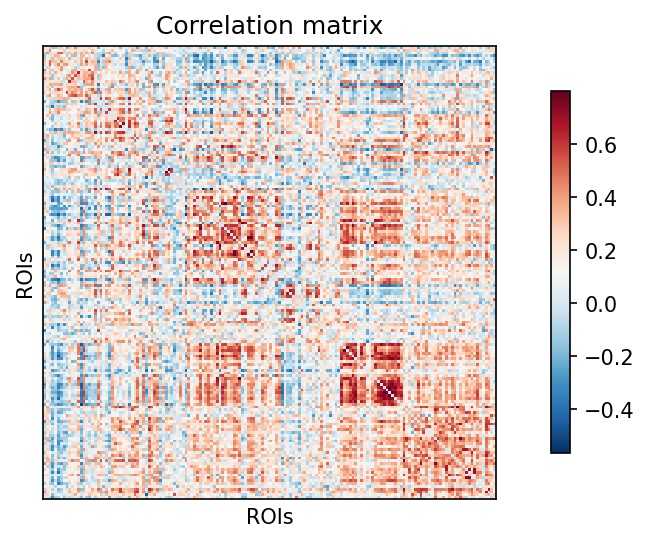
さらに、脳内のネットワークとして視覚化しましょう。

ここでは、例として Default Mode Network (DMN) の結合性を見てみます。

Python

index = np.where(networks == b'default')[0]
coords_array = np.array([list(coords) for coords in coordinates[index]])

plotting.plot_connectome(correlation_matrix[index][:,index], 
                         coords_array,
                         edge_threshold="80%", colorbar=True)
plotting.show()

3Dでも描画できます²。

Python

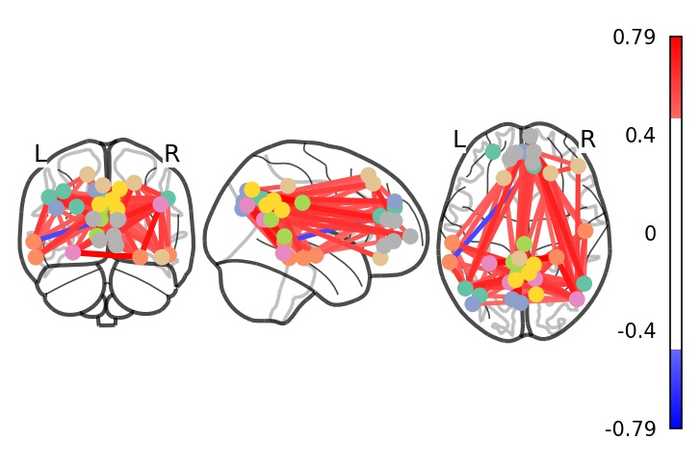
view = plotting.view_connectome(correlation_matrix[index][:,index],
                                coords_array,
                                node_size=5.0, edge_threshold='80%')
view.save_as_html("3d_connectome.html")
view

ネットワーク解析

まず、相関行列の上位10%のみを残して重みなしの隣接行列を作成します³。

Python

edge_threshold = np.percentile(connectome.sym_matrix_to_vec(correlation_matrix), 90)
adjacency_matrix = correlation_matrix.copy()
adjacency_matrix[adjacency_matrix >= edge_threshold] = 1
adjacency_matrix[adjacency_matrix != 1] = 0

plotting.plot_matrix(adjacency_matrix, colorbar=True, cmap='Greys')
plt.title("Adjacency matrix"); plt.xlabel("ROIs"); plt.ylabel("ROIs")
plt.xticks([]); plt.yticks([]); plt.show()

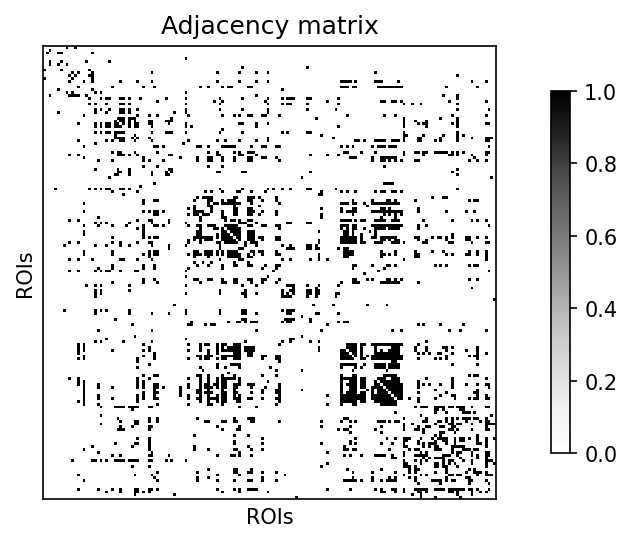
今回は、例としてクラスタリング係数 $CC$ という指標を計算しようと思います。

CC = \frac{1}{N} \sum_{i} \left( \frac{\sum_{j,k \in \Gamma_i} A_{j,k}^{(i)}}{d_i(d_i-1)} \right)

networkx⁴のグラフに変換して、クラスタリング係数を計算します。

Python

import networkx as nx

G = nx.from_numpy_matrix(adjacency_matrix)
print("the number of Nodes:", G.number_of_nodes())
clustering_coefficient = np.mean(list(nx.clustering(G).values()))
print("Clustering Coefficient: {:.3f}".format(clustering_coefficient))

Output

the number of Nodes: 160
Clustering Coefficient: 0.431

参考：CONN - Clustering Coefficient

以上となりますが、他にも信号の取得方法やグラフ指標などに様々な方法が利用されているので調べてみて下さい！

the Autism Brain Imaging Data Exchange ↩
ブラウザ上で自由に動かして見ることができます。↩
重み付き隣接行列を使用する場合もあります。↩
Pythonのグラフやネットワーク解析に特化したパッケージです。↩