PRML３章（３）ベイズモデル比較とエビデンス近似

最終更新日: 2020年5月29日

Jupyter Notebookはこちら

ベイズモデル比較

点推定の代わりに**周辺化**によってモデルのハイパーパラメータを評価しましょう。

Ｌ個の $Model = \{M_1, \ldots ,M_L\}$ に対し、あるモデルの不確かさはモデルの事後分布で評価できます。

p(M_i|Data)=p(M_i)p(Data|M_i)

このとき、 $p(Data|M_i)$ を**モデルエビデンス**といい、モデル空間におけるデータの周辺尤度となっています。

$\frac{p(Data|M_j)}{p(Data|M_k)}$ はベイズ因子と呼ばれ、仮説検定におけるエビデンスの強さを評価するのに使われています。

事後分布が求まれば、予測分布は以下のように求められます。

p(t|\vec{x},Data)=\sum_{i=1}^Lp(t|\vec{x},M_i,Data)p(M_i|Data)

①モデルエビデンスの解釈１

パラメータを事前分布からランダムにサンプリングしたときに、観測データが生成する確率。

p(Data|M_i)=\int p(Data|\vec{w},M_i)p(\vec{w}|M_i)d\vec{w}

②モデルエビデンスの解釈２

$p(Data|M_i)$ は、あるパラメーターの最頻値 $w_{MAP}$ で尖っているとき、

\left\{ \begin{array}{l} \int p(Data|w,M_i)dw \simeq p(Data|w_{MAP},M_i) \cdot \triangle w_{posterior}\\ p(w|M_i)\simeq \frac{1}{\triangle w_{prior}} \end{array} \right.

となるので、モデルエビデンスは以下のようになります。

p(Data|M_i)\simeq p(Data|w_{MAP},M_i) \frac{\triangle w_{posterior}}{\triangle w_{prior}}

\therefore \ln p(Data|M_i)\simeq \ln p(Data|w_{MAP},M_i) + \ln ({\frac{\triangle w_{posterior}}{\triangle w_{prior}}})

第１項はデータへの適合度を表し、第２項はモデルの複雑さによるペナルティを表しています。

エビデンス近似（経験ベイズ、第二種の最尤推定、一般化最尤推定）

**フルベイズ的**に扱うために、ハイパーパラメータ $\alpha,\beta$ にも事前分布を導入します。

p(t|\vec{t})=\iiint p(t|\vec{w},\beta)p(\vec{w}|\vec{t},\alpha,\beta)p(\alpha,\beta|\vec{t})d\vec{w}d\alpha d\beta

→ すべてのパラメータに対して解析的に周辺化することは難しい。
→ パラメータ $\vec{w}$ に関する周辺尤度を最大にするようにハイパーパラメータを決めましょう。

ベイズの定理から $p(\alpha,\beta|\vec{t}) \propto p(\vec{t}|\alpha,\beta)p(\alpha,\beta)$ なので、 $p(\vec{t}|\alpha,\beta)$ を最大にする $\hat{\alpha},\hat{\beta}$ を求めます。

$p(\vec{t}|\alpha,\beta)$ は**エビデンス関数**と呼ばれます。

p(\vec{t}|\alpha,\beta)=\int p(\vec{t}|\vec{w},\beta)p(\vec{w}|\beta)d\vec{w}

=\left(\frac{\beta}{2 \pi}\right)^\frac{N}{2}\left(\frac{\alpha}{2 \pi}\right)^\frac{M}{2}\int \exp\{-E(\vec{w})\}d\vec{w}

=\left(\frac{\beta}{2 \pi}\right)^\frac{N}{2}\left(\alpha \right)^\frac{M}{2}|A|^{-\frac{1}{2}} \exp\{-E(\vec{m_N})\}

と変形できるので、これを最大にする $\hat{\alpha}, \hat{\beta}$ を求めます。

ここで、以前の結果から以下のようにしています。

E(\vec{w})=\frac{\beta}{2}||\vec{t}-\Phi\vec{w}||^2-\frac{\alpha}{2}\vec{w}^T\vec{w}=E(\vec{m_N})+\frac{1}{2}(\vec{w}-\vec{m_N})^TA(\vec{w}-\vec{m_N})

\left\{ \begin{array}{l} A=\alpha I + \beta \Phi^T \Phi = \nabla \nabla E(\vec{w}) ：ヘッセ行列\\ \vec{m_N}=\beta A^{-1} \Phi^T \vec{t} \end{array} \right.

エビデンス関数の最大化

① $\alpha$ について最大化

$(\beta \Phi^T \Phi)\vec{u}_i=\lambda_i \vec{u}_i$ という固有方程式を考えます。

$A=\alpha I + \beta \Phi^T \Phi$ だから、これは固有値 $\alpha+\lambda_i$ を持つことになるので、

\frac{d}{d\alpha} \ln|A|=\frac{d}{d\alpha} \sum_{i} \ln(\alpha+\lambda_i)=\sum_{i}\frac{1}{\alpha+\lambda_i}

となるので、エビデンス関数の $\alpha$ に関する最大値（停留点）は、

\frac{d}{d\alpha} p(\vec{t}|\alpha,\beta) = 0

\therefore \frac{M}{2\alpha}-\frac{1}{2}\vec{m_N}^T\vec{m_N}-\frac{1}{2}\sum_{i}\frac{1}{\alpha+\lambda_i}= 0

\therefore \alpha = \frac{1}{\vec{m_N}^T\vec{m_N}} \left( M-\alpha\sum_{i}\frac{1}{\alpha+\lambda_i} \right) = \frac{1}{||m_N||^2} \sum_{i}\frac{\lambda_i}{\alpha+\lambda_i}

右辺は $\alpha$ に依存するから、これは $\alpha$ の陰関数。→ $\alpha_0$ から更新を繰り返して収束させます。

② $\beta$ について最大化

\frac{d}{d\beta} \ln|A|=\frac{d}{d\beta} \sum_{i} \ln(\alpha+\lambda_i) = \sum_{i} \frac{d\lambda_i}{d\beta}\frac{d}{d\lambda_i} \ln(\alpha+\lambda_i) =\frac{1}{\beta}\sum_{i}\frac{\lambda_i}{\alpha+\lambda_i}

よって、エビデンス関数の $\beta$ に関する最大値（停留点）は、

\frac{d}{d\beta} p(\vec{t}|\alpha,\beta) = 0

\therefore \frac{M}{2\beta}-\frac{1}{2}\sum_{n}\{t_n-\vec{m_N}^T\vec{\phi}\}^2 -\frac{1}{2\beta}\sum_{i}\frac{\lambda_i}{\alpha+\lambda_i}

\therefore \frac{1}{\beta}=\frac{1}{N-\sum_{i}\frac{\lambda_i}{\alpha+\lambda_i}}\sum_{n}\{t_n-\vec{m_N}^T\vec{\phi}\}^2

右辺は $\beta$ に依存するから、これは $\beta$ の陰関数。→ $\beta_0$ から更新を繰り返して収束させます。

エビデンス近似の実装

以上の手法を Python で実装します。初期値 $\alpha, \beta = 1$ から始めて収束するまで更新を繰り返します。

alpha=1.0
beta=1.0
N = 20
M = 10
tol=1e-4
maxiter=100
ary_mu = np.linspace(0,1,M)

x_real = np.arange(0, 1, 0.01)
y_real = np.sin(2*np.pi*x_real)

x_train = np.linspace(0,1,N)
y_train =  np.sin(2*np.pi*x_train) + np.random.normal(0,0.3,N)

def opt(Phi,t,tol,maxiter,alpha,beta):
    tmp_lambdas = eigh((Phi.T).dot(Phi))[0]
    cnt = 0
    while cnt < maxiter:
        lambdas = beta * tmp_lambdas
        S_ = inv(alpha * np.identity(M) + beta * (Phi.T).dot(Phi))
        m_ = beta * (S_.dot(Phi.T).dot(t.T))

        alpha_old = alpha
        beta_old = beta

        gamma = np.sum(lambdas/(alpha+lambdas))
        alpha = gamma/np.dot(m_,m_)
        beta = (len(t) - gamma) / norm(t - Phi.dot(m_)**2)

        if (abs(alpha - alpha_old)<tol)and(abs(beta-beta_old)<tol):
            break
        cnt += 1
    return alpha,beta

def phi(mus, x):
    ret = np.array([np.exp(-(x-mu)**2/(2*0.1**2)) for mu in mus])
    ret[0] = 1
    return ret

def pred(x_train, y_train,alpha,beta,ax):
    N = x_train.shape[0]
    PHI = np.array([phi(ary_mu,x) for x in x_train]).reshape(N,M)
    
    alpha,beta=opt(PHI,y_train,tol,maxiter,alpha,beta)
    S = inv(alpha * np.identity(M) + beta * (PHI.T).dot(PHI))
    m = beta * (S.dot(PHI.T).dot(y_train.T))

    PHI_real = np.array([phi(ary_mu,x) for x in x_real]).reshape(100,M)
    pred_mean = PHI_real.dot(m)
    pred_std = np.sqrt(1.0/beta + np.diag(PHI_real.dot(S).dot(PHI_real.T)))

    ax.plot(x_train, y_train, 'bo')
    ax.plot(x_real, y_real, 'g-')
    ax.plot(x_real, pred_mean, 'r-')
    ax.fill_between(x_real, pred_mean+pred_std, pred_mean-pred_std, color='pink')
    ax.set_xlim(0.0, 1.0)
    ax.set_ylim(-2, 2)
    ax.set_title('Evidence approximation(alpha={},beta={})'.format(round(alpha,3),round(beta,3)))

f,ax = plt.subplots(1,1,figsize=(6,4))
pred(x_train, y_train,alpha,beta,ax)

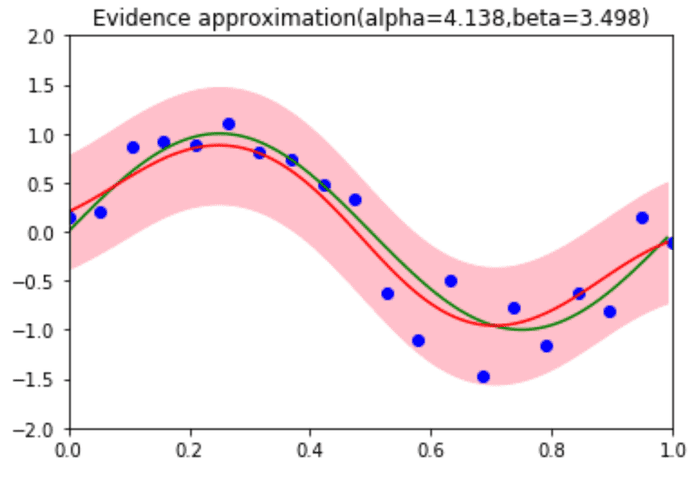
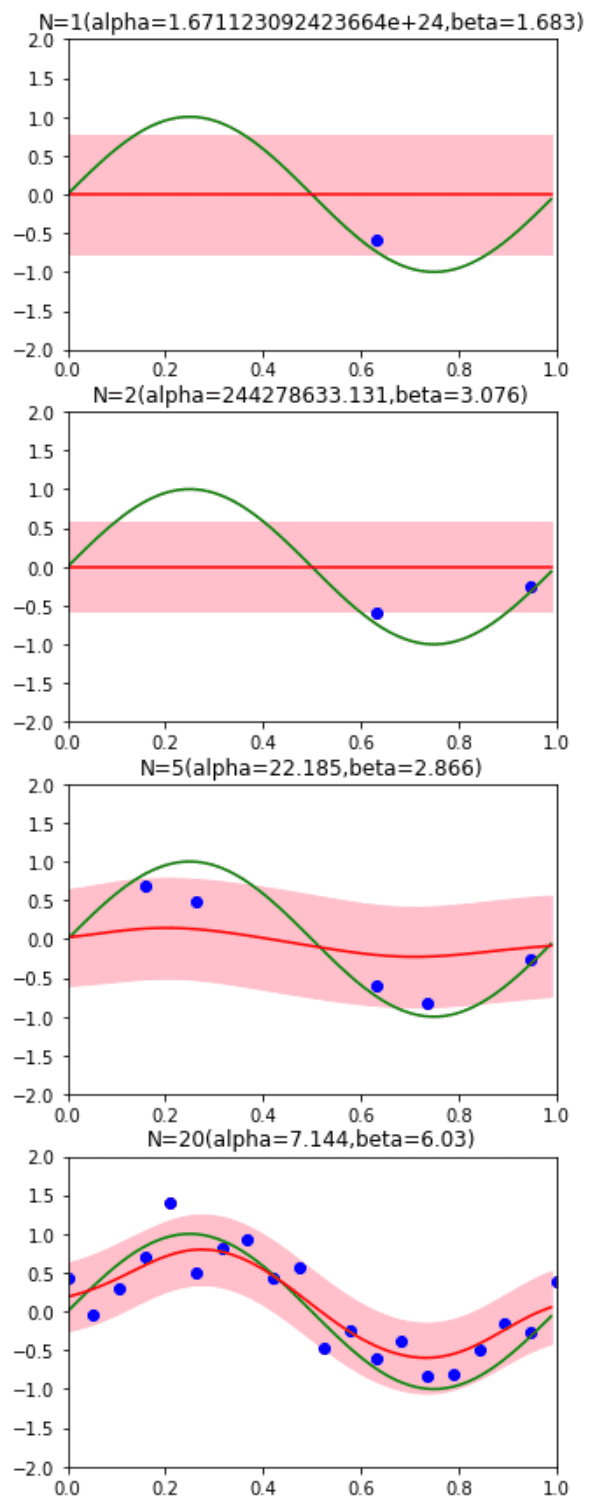
データ点の個数によるハイパーパラメータの違いを確認しましょう。データ点が少ない場合は最適化できていません。

alpha=1.0
beta=1.0
N = 20
M = 10
tol=1e-4
maxiter=100
ary_mu = np.linspace(0,1,M)

x_real = np.arange(0, 1, 0.01)
y_real = np.sin(2*np.pi*x_real)

x_train = np.linspace(0,1,N)
y_train =  np.sin(2*np.pi*x_train) + np.random.normal(0,0.3,N)

def opt(Phi,t,tol,maxiter,alpha,beta):
    tmp_lambdas = eigh((Phi.T).dot(Phi))[0]
    cnt = 0
    while cnt < maxiter:
        lambdas = beta * tmp_lambdas
        S_ = inv(alpha * np.identity(M) + beta * (Phi.T).dot(Phi))
        m_ = beta * (S_.dot(Phi.T).dot(t.T))

        alpha_old = alpha
        beta_old = beta

        gamma = np.sum(lambdas/(alpha+lambdas))
        alpha = gamma/np.dot(m_,m_)
        beta = (len(t) - gamma) / norm(t - Phi.dot(m_)**2)

        if (abs(alpha - alpha_old)<tol)and(abs(beta-beta_old)<tol):
            break
        cnt += 1
    return alpha,beta

def phi(mus, x):
    ret = np.array([np.exp(-(x-mu)**2/(2*0.1**2)) for mu in mus])
    ret[0] = 1
    return ret

def pred(x_train, y_train,alpha,beta,ax):
    N = x_train.shape[0]
    PHI = np.array([phi(ary_mu,x) for x in x_train]).reshape(N,M)
    
    alpha,beta=opt(PHI,y_train,tol,maxiter,alpha,beta)
    S = inv(alpha * np.identity(M) + beta * (PHI.T).dot(PHI))
    m = beta * (S.dot(PHI.T).dot(y_train.T))

    PHI_real = np.array([phi(ary_mu,x) for x in x_real]).reshape(100,M)
    pred_mean = PHI_real.dot(m)
    pred_std = np.sqrt(1.0/beta + np.diag(PHI_real.dot(S).dot(PHI_real.T)))

    ax.plot(x_train, y_train, 'bo')
    ax.plot(x_real, y_real, 'g-')
    ax.plot(x_real, pred_mean, 'r-')
    ax.fill_between(x_real, pred_mean+pred_std, pred_mean-pred_std, color='pink')
    ax.set_xlim(0.0, 1.0)
    ax.set_ylim(-2, 2)
    ax.set_title('N={}(alpha={},beta={})'.format(N,round(alpha,3),round(beta,3)))

f,axes = plt.subplots(4,1,figsize=(5,15))
r = np.arange(N)
np.random.shuffle(r)
for i,k in enumerate((1, 2, 5, N)):
    indices = np.sort(r[0:k]) 
    pred(x_train[indices], y_train[indices],alpha,beta,axes[i])

有効パラメータ数

$\gamma=\sum_{i}\frac{\lambda_i}{\alpha+\lambda_i}$ は、有効(well-determined)なパラメータの数 を表しています。

$\alpha$ を $0$ に変化させると、 $\gamma$ は $M$ に変化します。
→ $\alpha$ は、 $w_i$ の大きさを制御し、 $\gamma$ はデータに制約されるパラメータの数を表しています。
→ $N>M$ のとき（データ数がとても多い時）、すべての $w_i$ がwell-determinedとなります。

固定された基底関数の限界

基底関数を固定する欠点：次元の呪い

一般的には、データ集合に助けられています。

{ $\vec{x}_n$ } は、要素同士が強い相関を持ち、低次元の非線形多様体上に分布していることが多い
{ $t_n$ } は、多様体上の少数の方向に強く依存していることが多い

Reference

Bishop, Christopher M. Pattern recognition and machine learning. springer, 2006.