img-thumbnail

sn42

R&D Job in Japan.

Topics
My Twitter

PRML３章（１）線形回帰モデルと最尤推定

最終更新日: 2020年5月28日

Jupyter Notebookはこちら


回帰の目的 …… データ集合{xi}\{x_i\}から目標{ti}\{t_i\}を予測します。

線形基底関数モデル

単純にxix_iについて線形結合するのは「線形回帰」と呼ばれます。

y(x⃗,w⃗)=w0+w1x1+...+wDxDy(\vec{x},\vec{w}) = w_0 + w_1x_1 + ... + w_Dx_D

ここでは、xix_i について**非線形な関数の線形結合**を考えましょう。

y(x⃗,w⃗)=w0+∑j=1M−1wjϕj(x⃗)y(\vec{x},\vec{w}) = w_0 + \sum_{j=1}^{M-1}w_j \phi_j (\vec{x})

これは、パラメータwwについての線形結合なので「線形モデル」となります！

w0w_0は鬱陶しいので、ϕ0(x⃗)=1\phi_0(\vec{x}) = 1 とすれば、

y(x⃗,w⃗)=w⃗Tϕ⃗(x⃗) y(\vec{x},\vec{w}) = \vec{w}^T \vec{\phi} (\vec{x})

ただし、

x⃗=(x0⋮xD)w⃗=(w0⋮wM−1)ϕ⃗=(ϕ0⋮ϕM−1) \vec{x} = \left(\begin{array}{c} x_0 \\ \vdots \\ x_D \\ \end{array}\right) \quad \vec{w} = \left(\begin{array}{c} w_0 \\ \vdots \\ w_{M-1} \\ \end{array}\right) \quad \vec{\phi} = \left(\begin{array}{c} \phi_0 \\ \vdots \\ \phi_{M-1} \\ \end{array}\right) \quad

とします。w0w_0は「バイアスパラメータ」、ϕj(x⃗)\phi_j(\vec{x})は「基底関数」と呼びます。

基底関数の例

  1. ガウス基底関数

ϕj(x⃗)=exp⁡{−(x−μ)22s2}\phi_j (\vec{x}) = \exp \{-\frac{(x-\mu)^2}{2s^2}\}

  1. シグモイド基底関数

ϕj(x⃗)=11+exp⁡(x−μjs)=σ(x−μjs)\phi_j (\vec{x}) = \frac {1}{1+\exp(\frac{x-\mu_j}{s})} = \sigma(\frac{x-\mu_j}{s})

  1. フーリエ基底関数

ϕj(x⃗)=exp⁡(jnkx)\phi_j (\vec{x}) = \exp(jnkx)

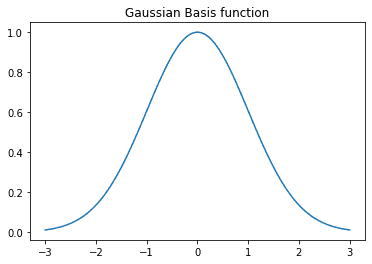
Gaussian Basis function

import numpy as np

def GBF(x,m,s):
    return np.exp(-(x - m)**2/(2*(s)**2))

gaussian.png

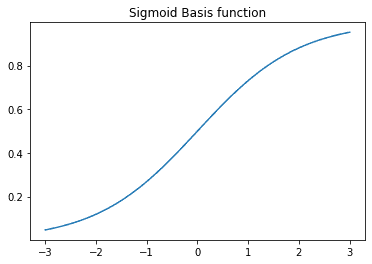
Sigmoid Basis fuction

import numpy as np

def SBF(x,m,s):
    return 1 / (1 + np.exp(-(x-m)/s))

sigmoid.png

最尤推定：最小二乗法で尤もらしい回帰モデルを推定しよう

t=y(x⃗,w⃗)+ε=(決定論的関数)+(ガウスノイズ) t = y(\vec{x},\vec{w}) + \varepsilon = (決定論的関数) + (ガウスノイズ)

目標変数 tt は決定論的関数とガウスノイズの和で表されるとしましょう。

ε∼N(ε∣0,β−1)\varepsilon \sim \mathcal{N}(\varepsilon |0,\beta^{-1})、つまりガウスノイズは平均 00 分散 β−1\beta^{-1} の正規分布に従うので、

p(t∣x⃗,w⃗,β)=N(t∣y(x⃗,w⃗),β−1)p(t|\vec{x},\vec{w},\beta) = \mathcal{N}(t|y(\vec{x},\vec{w}),\beta^{-1})

と表されます。また、新たなxnew⃗\vec{x_{new}}に対する予測値は、ttの条件付き期待値で与えられて、

E[t∣xnew⃗]=∫tp(t∣xnew⃗)dt=y(xnew⃗∣w⃗)\mathbb{E}[t|\vec{x_{new}}] = \int t p(t|\vec{x_{new}})dt = y(\vec{x_{new}}|\vec{w})

つまり、予測値はxnew⃗\vec{x_{new}}を**決定論的関数に代入する**ことで得られます。

次に、データ集合を考えます。

Data={x1⃗,…,xN⃗},t⃗=(t1,...,tN)Data = \{\vec{x_1}, \ldots ,\vec{x_N}\}, \vec{t} = (t_1,...,t_N) とするとき、

p(t⃗∣Data,w⃗,β)=∏n=1NN(tn∣w⃗Tϕ⃗(xn⃗),β−1) p(\vec{t}|Data,\vec{w},\beta) = \prod_{ n = 1 }^N \mathcal{N}(t_n|\vec{w}^T\vec{\phi}(\vec{x_n}),\beta^{-1})
∴ ln⁡p(t⃗∣w⃗,β)=∑n=1Nln⁡N(tn∣w⃗Tϕ⃗(xn⃗),β−1)　　　　　　　　=N2ln⁡β−N2ln⁡(2π)−βED(w⃗)\therefore \ \ln p(\vec{t}|\vec{w},\beta) = \sum_{ n = 1 }^N \ln \mathcal{N}(t_n|\vec{w}^T\vec{\phi}(\vec{x_n}),\beta^{-1}) \\ 　　　　　　　　 = \frac{N}{2}\ln\beta - \frac{N}{2}\ln(2\pi)-\beta E_D(\vec{w})

ただし、最小二乗誤差は、ED(w⃗)=12∑n=1N{tn−w⃗Tϕ⃗(xn⃗)}2E_D(\vec{w})=\frac{1}{2} \sum_{n=1}^N\{t_n - \vec{w}^T\vec{\phi}(\vec{x_n})\}^2です。

最尤推定をするために、対数尤度 ln⁡p(t⃗∣w⃗,β)\ln p(\vec{t}|\vec{w},\beta) を w⃗\vec{w} について最大化します。

w⃗\vec{w} に依存するのは ED(w⃗)E_D(\vec{w}) だけなので、これを最小化すればよいでしょう。

∇ln⁡p(t⃗∣w⃗,β)=0∴ β∑n=1N{tn−w⃗Tϕ⃗(xn⃗)}ϕ⃗(xn⃗)T=0∴ ∑n=1Ntnϕ⃗T−w⃗T(∑n=1Nϕ⃗⋅ϕ⃗T)=0∴ wML⃗=(∑n=1Nϕ⃗⋅ϕ⃗T)−1∑n=1Nϕ⃗ tn\nabla \ln p(\vec{t}|\vec{w},\beta) = 0 \\ \therefore \ \beta \sum_{n=1}^N \{ t_n - \vec{w}^T\vec{\phi}(\vec{x_n}) \}\vec{\phi}(\vec{x_n})^T = 0 \\ \therefore \ \sum_{n=1}^N t_n \vec{\phi}^T - \vec{w}^T(\sum_{n=1}^N\vec{\phi} \cdot \vec{\phi}^T) = 0 \\ \therefore \ \vec{w_{ML}} = (\sum_{n=1}^N\vec{\phi} \cdot \vec{\phi}^T)^{-1}\sum_{n=1}^N\vec{\phi} \ t_n \\

これは、**正規方程式**と呼ばれ、計画行列 Φ\Phi ・ペンローズの疑似逆行列 Φ†\Phi^\dagger を用いて表すことができます。

wML⃗=(ΦTΦ)−1ΦTt⃗=Φ†t⃗ \vec{w_{ML}} = (\Phi^T\Phi)^{-1}\Phi^T\vec{t} = \Phi^\dagger \vec{t}

ただし、計画行列 Φ\Phi は以下のように定義します。

Φ=(ϕ1(x1⃗)…ϕM−1(x1⃗)⋮⋱⋮ϕ1(xN⃗)…ϕM−1(xN⃗))\Phi = \left( \begin{array}{ccc} \phi_1(\vec{x_1}) & \ldots & \phi_{M-1}(\vec{x_1})\\ \vdots & \ddots & \vdots \\ \phi_1(\vec{x_N}) & \ldots & \phi_{M-1}(\vec{x_N}) \end{array} \right)

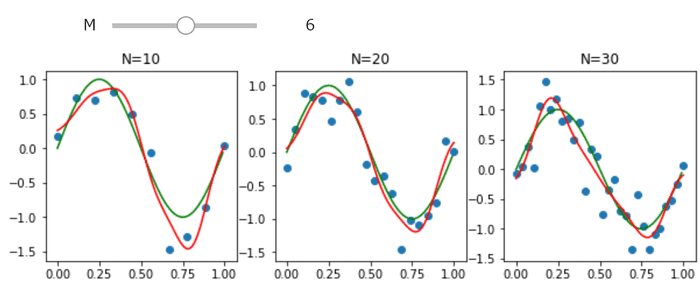
サイン関数＋ノイズによって生成されたサンプルに対し最尤推定をしましょう。Pythonによる実装は以下です。

import numpy as np
import matplotlib.pyplot as plt
from numpy.linalg import inv
from ipywidgets import interact

# 基底関数の実装
def phi(mus, x):
    ret = np.array([np.exp(-(x-mu)**2/(2*0.1**2)) for mu in mus])
    ret[0] = 1
    return ret

# 正規方程式を解く関数
def solve(mus,x_train,y_train,N,m):
    # 計画行列(3.16式)の計算
    PHI = np.array([phi(mus,x) for x in x_train]).reshape(N,m)
    # 最尤推定解(3.15式)の計算
    w_ml = inv(PHI.transpose().dot(PHI)).dot(PHI.transpose()).dot(y_train)
    return w_ml

# 真の関数はsin()
x_real = np.arange(0, 1, 0.01)
y_real = np.sin(2*np.pi*x_real)

@interact(M=(2,10))
def plot(M):
    ary_mu = np.linspace(0,1,M)

    f,ax = plt.subplots(1,3,figsize=(10,3))

    for i,N in enumerate([10,20,30]):
        ax[i].plot(x_real,y_real,'g-')

        x_train = np.linspace(0,1,N)
        y_train = np.sin(2*np.pi*x_train) + np.random.normal(0,0.3,N)
        ax[i].scatter(x_train,y_train,)

        w_ml = solve(ary_mu,x_train,y_train,N,M)

        x_range = np.linspace(0,1,100)
        ax[i].plot(x_range,[phi(ary_mu,x).dot(w_ml) for x in x_range],'r-')
        ax[i].set_title('N={}'.format(N))

linear_regress.png

バイアスパラメータ w0w_0 の役割

ED(w⃗)E_D(\vec{w})をw0w_0について最大化してみます。w0w_0を明示すると、

ED(w⃗)=12∑n=1N{tn−w0−∑j=1M−1wjϕj(xn⃗)}2E_D(\vec{w})= \frac{1}{2} \sum_{n=1}^N\{t_n - w_0 - \sum_{j=1}^{M-1}w_j \phi_j (\vec{x_n})\}^2

となるので、∂ED∂w0=0\frac{\partial E_D}{\partial w_0} = 0 としたとき、

w0=1N∑n=1Ntn−∑j=1M−1(wj1N∑n=1Nϕj(xn⃗))=tˉ−∑j=1M−1wjϕjˉw_0 = \frac{1}{N} \sum_{n=1}^N t_n - \sum_{j=1}^{M-1} (w_j \frac{1}{N} \sum_{n=1}^N \phi_j (\vec{x_n})) \\ = \bar{t} - \sum_{j=1}^{M-1} w_j \bar{\phi_j}

と表されます。したがって、

w0=(目標値の平均)−(基底の平均の重み付き線形和)w_0 = (目標値の平均) - (基底の平均の重み付き線形和)

となるため、w0w_0 はこの２つの差を埋める働きをしていることがわかります。

ノイズの精度 β\beta の役割

同様に、∂ED∂β=0\frac{\partial E_D}{\partial \beta} = 0 としたとき、

1βML=1N∑n=1N{tn−wML⃗Tϕ⃗(xn⃗)}2\frac{1}{\beta_{ML}} = \frac{1}{N}\sum_{n=1}^N\{t_n-\vec{w_{ML}}^T\vec{\phi}(\vec{x_n})\}^2

と表されます。したがって、

1βML=(残差の分散)\frac{1}{\beta_{ML}} = (残差の分散)

となるため、β\beta は残差の精度を表していることがわかります。

最小二乗法の意味

回帰関数は、M個の基底関数によって作られるM次元空間上の点となります。

よって、最小二乗誤差は、

ED=12∥(t1⋮tN)−(y(x1⃗,w⃗)⋮y(xN⃗,w⃗))∥2E_D = \frac{1}{2} \left\|{ \left(\begin{array}{c} t_1 \\ \vdots \\ t_N \\ \end{array}\right) - \left(\begin{array}{c} y(\vec{x_1},\vec{w}) \\ \vdots \\ y(\vec{x_N},\vec{w}) \\ \end{array}\right)} \right\|^2

と表され、目標値と回帰関数の**M次元空間上のユークリッド距離**となります。

逐次学習（オンライン学習）

大規模データの時は、一つずつデータを使ってパラメータを更新していくことが多いです。

このときの更新式は、

w⃗(t+1)=w⃗(t)+η∇En\vec{w}^{(t+1)} = \vec{w}^{(t)} + \eta\nabla E_n

とすればよいでしょう。この手法は、確率的勾配化法とも呼ばれています。

正則化最小二乗法

ΦTΦ\Phi^T\Phi が非正則に近いとき、逆行列が計算しにくくなり正規方程式が不安定となってしまいます。

これを防ぐために、誤差関数に正則化項を追加して正規性を保つようにすることがあります。

二乗誤差では、

E=12∑n=1N{tn−w⃗Tϕ⃗(xn⃗)}2+λ2w⃗⋅w⃗TE = \frac{1}{2} \sum_{n=1}^N\{t_n - \vec{w}^T\vec{\phi}(\vec{x_n})\}^2 + \frac{\lambda}{2} \vec{w} \cdot \vec{w}^T

という誤差を代わりに用います。このときの最尤推定値は、

wML⃗=(λI+ΦTΦ)−1ΦTt⃗ \vec{w_{ML}} = (\lambda I + \Phi^T\Phi)^{-1}\Phi^T\vec{t}

となります。この手法は「荷重減衰」や「パラメータ縮小推定」と呼ばれています。

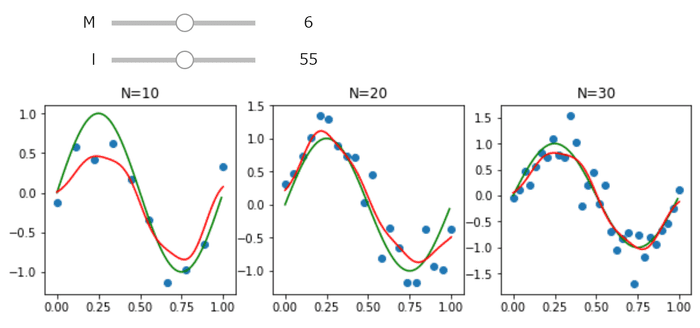
前回の手法に正則化項を加えましょう。Pythonによる実装は以下です。

def phi(mus, x):
    ret = np.array([np.exp(-(x-mu)**2/(2*0.1**2)) for mu in mus])
    ret[0] = 1
    return ret

def solve(mus,x_train,y_train,N,m,l_):
    PHI = np.array([phi(mus,x) for x in x_train]).reshape(N,m)
    # 正則化項を加える
    w_ml = inv(l_*np.identity(m)+PHI.transpose().dot(PHI)).dot(PHI.transpose()).dot(y_train)
    return w_ml

x_real = np.arange(0, 1, 0.01)
y_real = np.sin(2*np.pi*x_real)

@interact(M=(2,10),l=(10,100))
def plot(M,l):
    ary_mu = np.linspace(0,1,M)
    l *= 0.01

    f,ax = plt.subplots(1,3,figsize=(10,3))

    for i,N in enumerate([10,20,30]):
        ax[i].plot(x_real,y_real, 'g-')

        x_train = np.linspace(0,1,N)
        y_train = np.sin(2*np.pi*x_train) + np.random.normal(0,0.3,N)
        ax[i].scatter(x_train,y_train,)

        w_ml = solve(ary_mu,x_train,y_train,N,M,l)

        x_range = np.linspace(0,1,100)
        ax[i].plot(x_range,[phi(ary_mu,x).dot(w_ml) for x in x_range],'r-')
        ax[i].set_title('N={}'.format(N))

regu_regress.png

Reference

  • Bishop, Christopher M. Pattern recognition and machine learning. springer, 2006.
Topics
My Twitter