縮小ランクリッジ回帰とは？〜実装編〜

最終更新日: 2020年4月21日

簡単に！

「縮小ランク回帰」と「リッジ回帰」を組み合わせて、説明変数の共線性と目的変数の低次元構造に同時に適合するようにした、線形モデル回帰の手法。

ちなみに：詳しい理論はこちら

Step3. パッケージを試してみる

参考リンクのRRRRパッケージ内のデモを実行してみました。

１．データ

用意されていたデモ用のデータを使用しましょう。

Python

import numpy as np
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import PredefinedSplit
import reduced_rank_regressor as RRR

import matplotlib.pyplot as plt
%matplotlib inline

N_PARAMETERS_GRID_SEARCH = 20 
Data_path = "data/"

# Load Data
trainX = np.loadtxt(Data_path+"trainX.txt")
testX = np.loadtxt(Data_path+"testX.txt")
validX = np.loadtxt(Data_path+"validX.txt")

trainY = np.loadtxt(Data_path+"trainY.txt")
testY = np.loadtxt(Data_path+"testY.txt")
validY = np.loadtxt(Data_path+"validY.txt")

# Inspection of Data
f,ax = plt.subplots(1,2,figsize=(10,10))
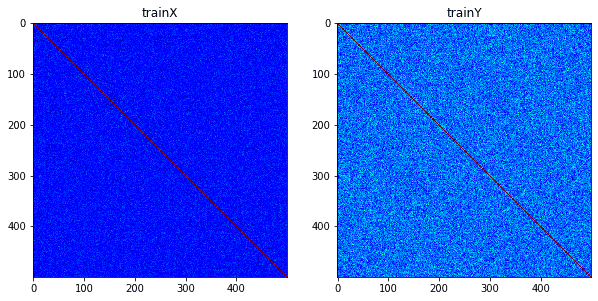
ax[0].imshow(np.corrcoef(trainX), cmap='jet')
ax[0].set_title('trainX')
ax[1].imshow(np.corrcoef(trainY), cmap='jet')
ax[1].set_title('trainY')
plt.show()

相関行列から、目的変数 $Y$ には低次元の構造があることがわかります。

２．交差検証

制約ランクと正則化の強さについてハイパーパラメータの交差検証を行い、最適化を行います。

Python

# Cross-validation setup. Define search spaces
rank_grid = np.linspace(1,min(min(trainX.shape),
                        min(trainY.shape)), num=N_PARAMETERS_GRID_SEARCH)
rank_grid = rank_grid.astype(int)
reg_grid = np.power(10,np.linspace(-20,20, num=N_PARAMETERS_GRID_SEARCH+1))
parameters_grid_search  = {'reg':reg_grid,
                           'rank':rank_grid}

valid_test_fold = np.concatenate((  np.zeros((trainX.shape[0],))-1,
                                    np.zeros((validX.shape[0],))  ))
ps_for_valid = PredefinedSplit(test_fold=valid_test_fold)

# Model initialisation
rrr = RRR.ReducedRankRegressor()#rank, reg)
grid_search = GridSearchCV(rrr, parameters_grid_search, cv=ps_for_valid,
                           scoring='neg_mean_squared_error')

print("fitting...")
grid_search.fit(np.concatenate((trainX,validX)), np.concatenate((trainY,validY)))

# Display the best combination of values found
print(grid_search.best_params_)
means = grid_search.cv_results_['mean_test_score']
means = np.array(means).reshape(N_PARAMETERS_GRID_SEARCH, N_PARAMETERS_GRID_SEARCH+1)
print('best score:',grid_search.best_score_)

[output]
fitting...
{'rank': 316, 'reg': 1e-20}
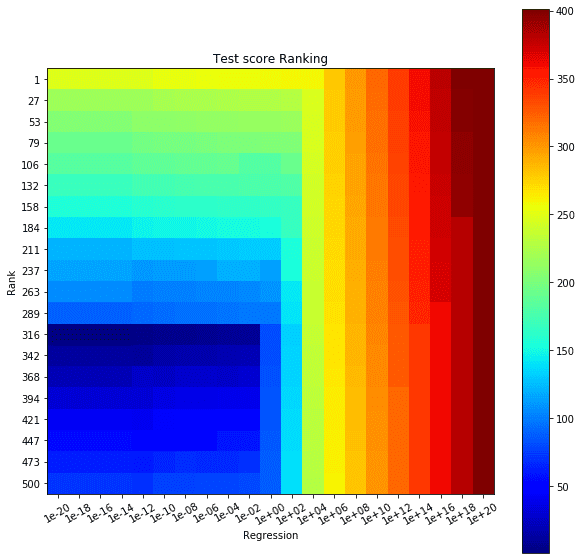
best score: -75126.47521541138

交差検証の結果について視覚化しましょう。最適ランクの部分(316付近)でスコアの順位が高くなっていることがわかります。

Python

# Show CV results
scores = [x for x in grid_search.cv_results_['rank_test_score']]
scores = np.array(scores).reshape(N_PARAMETERS_GRID_SEARCH,
                                    N_PARAMETERS_GRID_SEARCH+1)

f,ax = plt.subplots(1,1,figsize=(10,10))
cbar = ax.imshow(scores, cmap='jet')
ax.set_title('Test score Ranking')
ax.set_xlabel('Regression')
ax.set_ylabel('Rank')
ax.set_xticks(list(range(len(reg_grid))))
ax.set_yticks(list(range(len(rank_grid))))
ax.set_xticklabels([str("%0.*e"%(0,x)) for x in reg_grid],
                    rotation=30)
ax.set_yticklabels([str(x) for x in rank_grid])
f.colorbar(cbar)
plt.show()

３．推論

交差検証で求めた最適なハイパーパラメータを元に推論をします。

Python

# Train a model with the best set of hyper-parameters found
rrr.rank                = int(grid_search.best_params_['rank'])
rrr.reg                 = grid_search.best_params_['reg']
rrr.fit(trainX, trainY)

# Testing 
Yhat = rrr.predict(testX).real
MSE = (np.power((testY - Yhat),2)/np.prod(testY.shape)).mean()
print("MSE =",MSE)

f,ax = plt.subplots(1,2,figsize=(10,10))
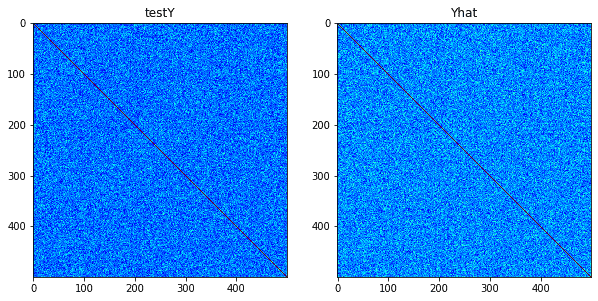
ax[0].imshow(np.corrcoef(testY), cmap='jet')
ax[0].set_title('testY')
ax[1].imshow(np.corrcoef(Yhat), cmap='jet')
ax[1].set_title('Yhat')
plt.show()

[output]
MSE = 0.1508996355795968

MSE（平均二乗誤差）は小さくなり、 $\hat{Y}$ はよく予測できていると思われます。

まとめ

縮小ランクリッジ回帰は低次元である目的変数に適合する能力が高く、現実のデータ構造に広く適用できるかもしれない！